Binäres Zahlensystem ist ein Zahlensystem, das verwendet wird, um verschiedene Zahlen mit nur zwei Symbolen, 0 und 1, darzustellen. Das Wort binär leitet sich vom Wort bi ab, was zwei bedeutet. Daher wird dieses Zahlensystem Binärzahlensystem genannt. Somit ist das binäre Zahlensystem ein System, das nur zwei Symbole hat.
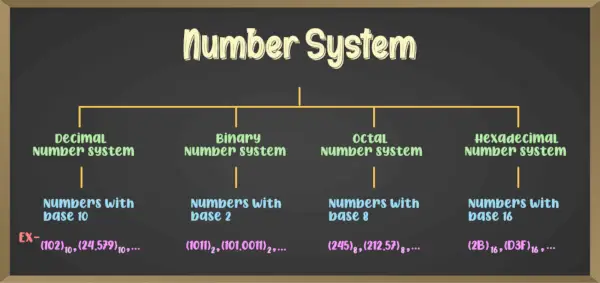
Im Allgemeinen gibt es verschiedene Arten von Zahlensystemen, von denen die vier wichtigsten sind:
- Binäres Zahlensystem (Zahlensystem mit Basis 2)
- Oktales Zahlensystem (Zahlensystem mit Basis 8)
- Dezimalzahlensystem (Zahlensystem mit Basis 10)
- Hexadezimales Zahlensystem (Zahlensystem mit Basis 16)
Hier werden wir nur etwas über das binäre Zahlensystem lernen. Dieses Zahlensystem ist sehr nützlich, um dem Computer Aufgaben zu erklären. Im Binärzahlensystem haben wir zwei Zustände 0 und 1 und diese beiden Zustände werden durch zwei Zustände eines Transistors dargestellt. Wenn der Strom durch den Transistor fließt, zeigt der Computer 1 an, und wenn kein Strom durch den Transistor fließt, zeigt er 0 an. Wenn der Strom also abgewechselt wird, liest der Computer das binäre Zahlensystem. Jede Ziffer im binären Zahlensystem wird als Bit bezeichnet.
In diesem Artikel lernen wir das Binärzahlensystem, die Konvertierung des Binärzahlensystems, die Binärtabelle, die Funktionsweise von Binärzahlen, Beispiele und vieles mehr im Detail kennen.
Inhaltsverzeichnis
- Binäres Zahlensystem
- Binärzahlentabelle
- Binär-Dezimal-Konvertierung
- Dezimal-Binär-Konvertierung
- Arithmetische Operationen mit Binärzahlen
- 1er- und 2er-Komplement einer Binärzahl
- Verwendung des binären Zahlensystems
- Beispiel für ein Binärzahlensystem
Binäres Zahlensystem
Das binäre Zahlensystem ist das Zahlensystem, in dem wir zwei Ziffern 0 und 1 verwenden, um alle notwendigen Operationen durchzuführen. Im Binärzahlensystem haben wir eine Basis von 2. Die Basis des Binärzahlensystems wird auch Basis von 2 genannt Zahlensystem .
In einem binären Zahlensystem stellen wir die Zahl dar als:
- (11001)2
Im obigen Beispiel ist eine Binärzahl angegeben, deren Basis 2 ist. In einem Binärzahlensystem wird jede Ziffer als Bit bezeichnet. Im obigen Beispiel sind es 5 Ziffern.
Binärzahlentabelle
| Dezimalzahl | Binäre Zahl | Dezimalzahl | Binäre Zahl |
|---|---|---|---|
| 1 | 001 | elf | 1011 vergleiche mit string |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | fünfzehn | 1111 |
| 6 | 110 | 16 | 10000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 | zwanzig | 10100 |
Binär-Dezimal-Konvertierung
Eine Binärzahl wird in eine Dezimalzahl umgewandelt, indem jede Ziffer der Binärzahl mit der Potenz von 1 oder 0 mit der entsprechenden Potenz von 2 multipliziert wird. Nehmen wir an, dass eine Binärzahl n Ziffern hat, B = an-1…A3A2A1A0. Nun wird die entsprechende Dezimalzahl angegeben als
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Lassen Sie uns ein Beispiel durchgehen, um das Konzept besser zu verstehen.
Beispiel: Konvertieren (10011) 2 in eine Dezimalzahl umwandeln.
Lösung:
Die angegebene Binärzahl ist (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Daher ist die Binärzahl (10011)2wird ausgedrückt als (19)10.
Dezimal-Binär-Konvertierung
Eine Dezimalzahl wird in eine Binärzahl umgewandelt, indem man die gegebene Dezimalzahl kontinuierlich durch 2 dividiert, bis der Quotient 1 ist, und wir schreiben die Zahlen von unten nach oben.
Lassen Sie uns ein Beispiel durchgehen, um das Konzept besser zu verstehen.
Beispiel: Konvertieren (28) 10 in eine Binärzahl umwandeln.
Lösung:
Daher (28)10wird ausgedrückt als (11100)2.
Arithmetische Operationen mit Binärzahlen
Wir können problemlos verschiedene Operationen an Binärzahlen durchführen. Verschiedene arithmetische Operationen auf der Binärzahl umfassen:
- Binäre Addition
- Binäre Subtraktion
- Binäre Multiplikation
- Binäre Division
Lassen Sie uns nun mehr darüber im Detail erfahren.
Binäre Addition
Das Ergebnis der Addition zweier Binärzahlen ist ebenfalls eine Binärzahl. Um das Ergebnis der Addition zweier Binärzahlen zu erhalten, müssen wir die Ziffern der Binärzahlen ziffernweise addieren. Die unten hinzugefügte Tabelle zeigt die Regel der binären Addition.
| Binärzahl (1) | Binärzahl (2) | Zusatz | Tragen |
|---|---|---|---|
| 0 | 0 | 0 | 0 CSS-Kommentar |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Binäre Subtraktion
Das Ergebnis der Subtraktion zweier Binärzahlen ist ebenfalls eine Binärzahl. Um das Ergebnis der Subtraktion zweier Binärzahlen zu erhalten, müssen wir die Binärzahlen ziffernweise subtrahieren. Die unten hinzugefügte Tabelle zeigt die Regel der binären Subtraktion.
| Binärzahl (1) | Binärzahl (2) | Subtraktion | Ausleihen |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Binäre Multiplikation
Der Multiplikationsprozess von Binärzahlen ähnelt der Multiplikation von Dezimalzahlen. Die Regeln zum Multiplizieren zweier beliebiger Binärzahlen sind in der Tabelle aufgeführt.
| Binärzahl (1) | Binärzahl (2) | Multiplikation |
|---|---|---|
| 0 | 0 dritte Normalform | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Binäre Division
Der Teilungsmethode für Binärzahlen ähnelt der Methode der dezimalen Zahlendivision. Lassen Sie uns ein Beispiel durchgehen, um das Konzept besser zu verstehen.
Beispiel: Teilen (101101) 2 von (110) 2
Lösung:
1er- und 2er-Komplement einer Binärzahl
- Das 1er-Komplement einer Binärzahl erhält man durch Invertieren der Ziffern der Binärzahl.
Beispiel: Finden Sie das 1er-Komplement von (10011) 2 .
Lösung:
Die gegebene Binärzahl ist (10011)2
Um nun das 1er-Komplement zu finden, müssen wir die Ziffern der gegebenen Zahl invertieren.
Somit ist das 1er-Komplement von (10011)2ist (01100)2
- Das 2er-Komplement einer Binärzahl erhält man durch Invertieren der Ziffern der Binärzahl und anschließendes Addieren von 1 zum niedrigstwertigen Bit.
Beispiel: Finden Sie das 2er-Komplement von (1011) 2 .
Lösung:
Die gegebene Binärzahl ist (1011)2
Um das 2er-Komplement zu finden, ermitteln Sie zunächst das 1er-Komplement, d. h. (0100)2
Indem wir nun 1 zum niedrigstwertigen Bit addieren, erhalten wir (0101)2
Daher ist das 2er-Komplement von (1011)2ist (0101)2
Verwendung des binären Zahlensystems
Binäre Zahlensysteme werden für verschiedene Zwecke verwendet und die wichtigste Verwendung des binären Zahlensystems ist:
- Das Binärzahlensystem wird in der gesamten digitalen Elektronik zur Durchführung verschiedener Operationen verwendet.
- Programmiersprachen verwenden das Binärzahlensystem zum Kodieren und Dekodieren von Daten.
- Das Binärzahlensystem wird in den Datenwissenschaften für verschiedene Zwecke usw. verwendet.
Mehr lesen,
- Binäre Formel
- Unterschied zwischen dezimalen und binären Zahlensystemen
Beispiel für ein Binärzahlensystem
Beispiel 1: Dezimalzahl konvertieren (98) 10 in Binär.
Lösung:
dfs-Algorithmus
Somit ist die Binärzahl für (98)10ist gleich (1100010)2
Beispiel 2: Binärzahl konvertieren (1010101) 2 zur Dezimalzahl.
Lösung:
Gegebene Binärzahl, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 ×26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Somit ist die Binärzahl (1010101)2ist gleich (85)10im Dezimalsystem.
Beispiel 3: Teilen (11110) 2 von (101) 2
Lösung:
Beispiel 4: Hinzufügen (11011) 2 und (10100) 2
Lösung:
Daher (11011)2+ (10100)2= (101111)2
Beispiel 5: Subtrahieren (11010) 2 und (10110) 2
Lösung:
Daher (11010)2– (10110)2= (00100)2
Beispiel 6: Multiplizieren (1110) 2 und (1001) 2 .
Lösung:
Also (1110)2× (1001)2= (1111110)2
FAQs zum binären Zahlensystem
Was ist ein binäres Zahlensystem?
Das binäre Zahlensystem ist eines der vier Zahlensysteme, das zur Darstellung von Zahlen mit nur zwei Ziffern, 0 und 1, verwendet wird. Im binären Zahlensystem werden die Ziffern „Bits“ genannt. Das binäre Zahlensystem wird von Computern zur Durchführung verschiedener Berechnungen verwendet.
Was ist ein B Es?
Ein Bit im Binärzahlensystem ist als einzelne Ziffer definiert, die den Wert „0“ oder „1“ enthält.
Was ist ein Knabbern?
Eine Gruppe von vier Ziffern wird Niblle genannt.
Was ist der Binärwert von 10?
Der Binärwert von 10 ist (1010)2
Welche Arten von Zahlensystemen gibt es?
Es gibt verschiedene Arten von Zahlensystemen und einige davon sind:
- Binäres Zahlensystem
- Oktales Zahlensystem
- Dezimalzahlensystem
- Hexadezimales Zahlensystem
Wie berechnet man Binärzahlen?
Binärzahlen werden aus Dikmalzahlen berechnet, indem man die Dezimalzahl durch 2 dividiert und den Rest schreibt. Dann ordnen wir alle Reste vom neuesten zum ältesten, um die Binärzahl zu erhalten.
Wie füge ich Binärzahlen hinzu?
Binärzahlen werden mithilfe der unten aufgeführten Formeln addiert:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (Übertrag 1)






