Der Ford-Fulkerson-Algorithmus ist ein weit verbreiteter Algorithmus zur Lösung des Maximum-Flow-Problems in einem Flussnetzwerk. Das Problem des maximalen Flusses besteht darin, die maximale Flussmenge zu bestimmen, die von einem Quellscheitelpunkt zu einem Senkenscheitelpunkt in einem gerichteten gewichteten Diagramm gesendet werden kann, vorbehaltlich Kapazitätsbeschränkungen an den Kanten.
Der Algorithmus funktioniert, indem er iterativ einen Erweiterungspfad findet, der ein Pfad von der Quelle zur Senke im Restgraphen ist, d. h. dem Graphen, der durch Subtrahieren des Stromflusses von der Kapazität jeder Kante erhalten wird. Der Algorithmus erhöht dann den Fluss entlang dieses Pfads um den maximal möglichen Betrag, der der minimalen Kapazität der Kanten entlang des Pfads entspricht.
Problem:
Gegeben sei ein Diagramm, das ein Flussnetzwerk darstellt, in dem jede Kante eine Kapazität hat. Außerdem sind zwei Eckpunkte gegeben Quelle 's' und Waschbecken Finden Sie im Diagramm „t“ den maximal möglichen Fluss von s nach t mit den folgenden Einschränkungen:
- Der Fluss an einer Kante überschreitet nicht die angegebene Kapazität der Kante.
- Der eingehende Fluss ist für jeden Scheitelpunkt außer s und t gleich dem ausgehenden Fluss.
Betrachten Sie beispielsweise die folgende Grafik aus dem CLRS-Buch.
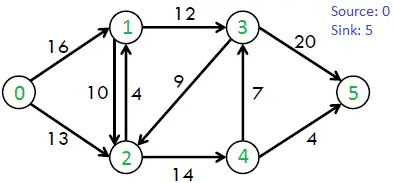
Der maximal mögliche Durchfluss in der obigen Grafik beträgt 23.

Voraussetzung: Einführung in das Max-Flow-Problem
Ford-Fulkerson-Algorithmus
Das Folgende ist eine einfache Idee des Ford-Fulkerson-Algorithmus:
- Beginnen Sie mit dem anfänglichen Durchfluss als 0.
- Es gibt zwar einen Erweiterungspfad von der Quelle zur Senke:
- Finden Sie einen Erweiterungspfad mithilfe eines beliebigen Pfadfindungsalgorithmus, z. B. der Breitensuche oder der Tiefensuche.
- Bestimmen Sie die Flussmenge, die entlang des Erweiterungspfads gesendet werden kann. Dies ist die minimale Restkapazität entlang der Pfadränder.
- Erhöhen Sie den Fluss entlang des Augmentierungspfads um den ermittelten Betrag.
- Gibt den maximalen Durchfluss zurück.
Zeitkomplexität: Die zeitliche Komplexität des obigen Algorithmus beträgt O(max_flow * E). Wir führen eine Schleife aus, solange es einen Erweiterungspfad gibt. Im schlimmsten Fall können wir in jeder Iteration einen Einheitsfluss hinzufügen. Daher wird die Zeitkomplexität O(max_flow * E).
Wie implementiert man den oben genannten einfachen Algorithmus?
Definieren wir zunächst das Konzept des Residualgraphen, das zum Verständnis der Implementierung erforderlich ist.
Restdiagramm eines Strömungsnetzwerks ist ein Diagramm, das zusätzliche mögliche Strömungen anzeigt. Wenn es im Restdiagramm einen Pfad von der Quelle zur Senke gibt, ist es möglich, einen Fluss hinzuzufügen. Jede Kante eines Residuengraphen hat einen Wert namens Restkapazität Dies entspricht der ursprünglichen Kapazität der Kante abzüglich des Stromflusses. Die Restkapazität ist im Grunde die aktuelle Kapazität der Kante.
Lassen Sie uns nun über die Implementierungsdetails sprechen. Die Restkapazität ist 0, wenn zwischen zwei Eckpunkten des Restgraphen keine Kante vorhanden ist. Wir können den Restgraphen als Originalgraphen initialisieren, da es keinen anfänglichen Durchfluss gibt und die Restkapazität zunächst gleich der Originalkapazität ist. Um einen Erweiterungspfad zu finden, können wir entweder eine BFS oder eine DFS des Restgraphen durchführen. Wir haben BFS in der folgenden Implementierung verwendet. Mithilfe von BFS können wir herausfinden, ob es einen Pfad von der Quelle zur Senke gibt. BFS erstellt auch ein übergeordnetes[]-Array. Mithilfe des Arrays parent[] durchlaufen wir den gefundenen Pfad und finden einen möglichen Fluss durch diesen Pfad, indem wir die minimale Restkapazität entlang des Pfads ermitteln. Später fügen wir den gefundenen Pfadfluss zum Gesamtfluss hinzu.
Wichtig ist, dass wir die Restkapazitäten im Restdiagramm aktualisieren müssen. Wir subtrahieren den Pfadfluss von allen Kanten entlang des Pfads und fügen den Pfadfluss entlang der umgekehrten Kanten hinzu. Wir müssen den Pfadfluss entlang der umgekehrten Kanten hinzufügen, da der Fluss später möglicherweise in umgekehrter Richtung gesendet werden muss (siehe folgenden Link zum Beispiel).
Nachfolgend finden Sie die Implementierung des Ford-Fulkerson-Algorithmus. Der Einfachheit halber wird der Graph als 2D-Matrix dargestellt.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Wenn wir eine Verbindung zum Senkenknoten finden, // dann hat BFS keinen Sinn mehr. Wir // müssen nur noch seinen übergeordneten Knoten festlegen und können // true zurückgeben, wenn (v == t) { parent[ v] = u; return true; } q.push(v); parent[v] = u; besucht[v] = true; } } } // Wir haben die Senke in BFS ausgehend von der Quelle nicht erreicht, also // return false return false; } // Gibt den maximalen Fluss von s nach t im angegebenen Diagramm zurück int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Erstelle einen Restgraphen und fülle den Restgraphen // mit gegebenen Kapazitäten im Originalgraphen als // Restkapazitäten im Restgraphen int rGraph[V] [V]; // Restgraph, wobei rGraph[i][j] // die Restkapazität der Kante // von i bis j angibt (wenn es eine Kante gibt. Wenn // rGraph[i][j] 0 ist, dann gibt es keine) for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; int parent[V]; // Dieses Array wird von BFS gefüllt und // zum Speicherpfad int max_flow = 0; // Anfänglich gibt es keinen Fluss. // Erweitern Sie den Fluss, solange ein Pfad von der Quelle zur // Senke vorhanden ist. while (bfs(rGraph, s, t, parent)) { // Finden Sie die minimale Restkapazität der Kanten entlang // des von BFS gefüllten Pfades. Oder wir können sagen: Finden Sie den // maximalen Fluss durch den gefundenen Pfad parent[v]; path_flow = min(path_flow, rGraph[u][v]); // Restkapazitäten der Kanten aktualisieren und // Kanten entlang des Pfades umkehren für (v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow } // Pfadfluss zum Gesamtfluss hinzufügen max_flow += path_flow } // Gesamtfluss zurückgeben return max_flow; } // Treiberprogramm zum Testen der oben genannten Funktionen int main() { // Lassen Sie uns ein Diagramm erstellen, das im obigen Beispiel gezeigt wird int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
c#-Schalter
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Wenn wir eine Verbindung zum Senkenknoten // finden, dann macht BFS // keinen Sinn mehr. Wir müssen nur noch dessen Elternknoten // festlegen und können true zurückgeben, wenn (v == t) { parent[ v] = u; return true; } queue.add(v); parent[v] = u; besucht[v] = wahr; } } } // Wir haben die Senke in BFS ausgehend von der Quelle nicht erreicht, // also return false return false; } // Gibt den maximalen Fluss von s nach t im gegebenen // Diagramm zurück int fordFulkerson(int graph[][], int s, int t) { int u, v; // Erstelle einen Restgraphen und fülle den Restgraphen // mit gegebenen Kapazitäten im Originalgraphen // als Restkapazitäten im Restgraphen // Restgraphen, wobei rGraph[i][j] die // Restkapazität der Kante von i bis angibt j (wenn es // eine Kante gibt. Wenn rGraph[i][j] 0 ist, dann gibt es // keine) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; // Dieses Array wird von BFS gefüllt und zum Speichern des Pfads int parent[] = new int[ V]; int max_flow = 0; // Es gibt anfangs keinen Fluss. // Erweitern Sie den Fluss, solange es einen Pfad von der Quelle // zur Senke gibt. while (bfs(rGraph, s, t, parent)) { // Finden Sie die minimale Restkapazität der Kanten // entlang des von BFS gefüllten Pfades. Oder wir können sagen: // Finden Sie den maximalen Fluss durch den gefundenen Pfad. int path_flow = Integer.MAX_VALUE; ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v] } // Restkapazitäten der Kanten aktualisieren und // Kanten entlang des Pfads umkehren für (v = t; v != s; v = parent[v]) { u = parent[v]; -= rGraph[v][u] += path_flow; flow max_flow += path_flow; } // Den Gesamtfluss zurückgeben return max_flow; } // Treiberprogramm zum Testen der oben genannten Funktionen public static void main(String[] args) throws java.lang.Exception { // Lassen Sie uns ein Diagramm erstellen im obigen Beispiel int graph[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = new MaxFlow(); System.out.println('Der maximal mögliche Fluss ist ' + m.fordFulkerson(graph, 0, 5)); } }> |
>
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Wenn wir eine Verbindung zum Senkenknoten // finden, dann macht BFS // keinen Sinn mehr. Wir müssen nur noch dessen Elternknoten // festlegen und können true zurückgeben, wenn (v == t) { parent[ v] = u; return true; } queue.push(v); parent[v] = u; besucht[v] = wahr; } } } // Wir haben die Senke in BFS ausgehend von // der Quelle nicht erreicht, also return false return false; } // Gibt den maximalen Fluss von s nach t in // der gegebenen Graphfunktion zurück fordFulkerson(graph, s, t) { let u, v; // Erstelle ein Restdiagramm und fülle das // Restdiagramm mit gegebenen Kapazitäten // im ursprünglichen Diagramm als Rest // Kapazitäten im Restdiagramm // Restdiagramm, wobei rGraph[i][j] // die Restkapazität der Kante angibt / / von i nach j (wenn es eine Kante gibt. // Wenn rGraph[i][j] 0 ist, dann gibt es // keine) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Dieses Array wird gefüllt mit BFS und zum Speichern des Pfads let parent = new Array(V); // Es gibt zunächst keinen Fluss let max_flow = 0; // Erweitern Sie den Fluss, solange // ein Pfad von der Quelle zur Senke vorhanden ist while (bfs(rGraph, s, t , parent)) { // Finden Sie die minimale Restkapazität der Kanten // entlang des von BFS gefüllten Pfads. // Finden Sie den maximalen Fluss durch den gefundenen Pfad ; v != s; v = parent[v]) { u = parent[v]; Kanten entlang des Pfades umkehren for(v = t; v != s; v = parent[v]) { u = parent[u][v] -= path_flow; = path_flow; } // Pfadfluss zum Gesamtfluss hinzufügen max_flow += path_flow } // Den Gesamtfluss zurückgeben return max_flow } // Treibercode // Erstellen wir ein im obigen Beispiel gezeigtes Diagramm let graph = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ] ]; document.write('Der maximal mögliche Fluss ist ' + fordFulkerson(graph, 0, 5)); // Dieser Code wurde von avanitrachhadiya2155>'> beigesteuert |
>The maximum possible flow is 23>
Zeitkomplexität: O(|V| * E^2) ,wobei E die Anzahl der Kanten und V die Anzahl der Eckpunkte ist.
Raumkomplexität :O(V) , als wir eine Warteschlange erstellt haben.
Die obige Implementierung des Ford-Fulkerson-Algorithmus heißt Edmonds-Karp-Algorithmus . Die Idee von Edmonds-Karp besteht darin, BFS in der Ford-Fulkerson-Implementierung zu verwenden, da BFS immer einen Pfad mit einer minimalen Anzahl von Kanten wählt. Wenn BFS verwendet wird, kann die Zeitkomplexität im ungünstigsten Fall auf O(VE) reduziert werden2). Die obige Implementierung verwendet jedoch eine Adjazenzmatrixdarstellung, wobei BFS O(V) verwendet2) Zeit beträgt die zeitliche Komplexität der obigen Implementierung O(EV3) (Verweisen CLRS-Buch zum Nachweis der Zeitkomplexität)
Dies ist ein wichtiges Problem, da es in vielen praktischen Situationen auftritt. Beispiele hierfür sind die Maximierung des Transports bei gegebenen Verkehrsbeschränkungen und die Maximierung des Paketflusses in Computernetzwerken.
Dincs Algorithmus für Max-Flow.
Übung:
Ändern Sie die obige Implementierung so, dass sie in O(VE) ausgeführt wird2) Zeit.
