Horizontale Linien werden als Linien definiert, die parallel zum Horizont oder zum Boden verlaufen, daher der Name horizontale Linie . Die horizontale Linie hat eine Neigung von Null, d. h. der Neigungswinkel dieser Linien beträgt null Grad. Wenn die horizontalen Linien auf den kartesischen Ebenen gezeichnet werden, schneiden sie sich nur entlang der y-Achse, da sie immer parallel zur x-Achse verlaufen und diese niemals schneiden.
In diesem Artikel erfahren Sie mehr über die horizontale Linie, ihre Eigenschaften, die Steigung der horizontalen Linie, die Gleichung der horizontalen Linie, Beispiele und häufig gestellte Fragen zu den horizontalen Linien und vieles mehr im Detail.
Inhaltsverzeichnis
- Horizontale Liniendefinition
- Steigung der horizontalen Linie
- Eine horizontale Linie zeichnen
- Horizontale Liniengleichung
- Horizontaler Linientest
- Horizontale und vertikale Linien
- Unterschiede zwischen vertikalen und horizontalen Linien
- Kurze Anmerkung zur horizontalen Linie
- Beispiele für horizontale Linien
Horizontale Liniendefinition
Wir wissen, dass eine Linie ein gerader Weg ist, der zwei oder mehr Punkte verbindet und bis ins Unendliche reicht. Daher definieren wir horizontale Linien als Linien, die parallel zum Boden oder zum Horizont verlaufen und eine konstante Höhe über dem Boden haben.
Wenn wir diese Linien im kartesischen System zeichnen, dann sind diese Linien die Linien, die keinen Schnittpunkt auf der x-Achse, aber einen Schnittpunkt auf der y-Achse haben. Horizontale Linien haben eine Neigung von Null, d. h. sie haben keinen Winkel zur x-Achse oder zum Boden.
Horizontale Linien bilden die Basis der verschiedenen Objekte, Formen und Figuren, die wir in der Geometrie studieren. Angenommen, wir müssen ein Rechteck, ein Quadrat, ein Dreieck zeichnen. Trapez usw., dann sind die Basis dieser Figuren meist horizontale Linien. Wir beobachten horizontale Lügen auch im wirklichen Leben, da die Linien auf dem Boden und der Decke der Räume, am Fuß der Treppe usw. ebenfalls durch horizontale Linien gebildet werden.
Diese Leinen werden auch als Schlafleinen bezeichnet, da sie keine vertikale Bewegung aufweisen und immer eine konstante Höhe über dem Boden haben. Das unten hinzugefügte Bild zeigt die horizontale Linie.
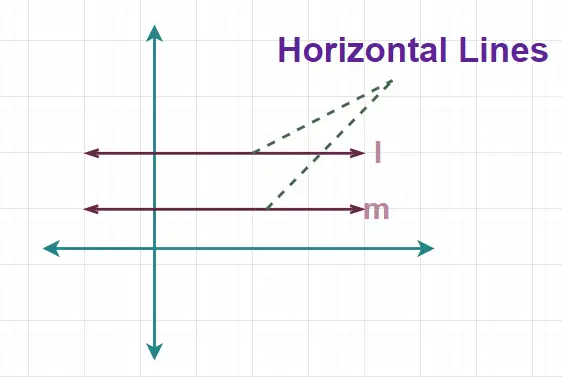
Hier sind in der oben hinzugefügten Abbildung die Linien l und m horizontale Linien.
Steigung der horizontalen Linie
Wir haben bereits erwähnt, dass die Steigung der horizontalen Linie Null ist . Lassen Sie uns nun lernen, dass die Steigung der horizontalen Linie Null ist. Wir berechnen die Steigung einer horizontalen Linie mithilfe der Formel:
Steigung = Anstieg/Lauf
ODER
Steigung der Linie = Änderung der Y-Koordinate/Änderung der X-Koordinate
Dabei ist „Rise“ die Höhe, die die Linie gewinnt, wenn sie von links nach rechts verläuft. Da wir bereits wissen, dass die horizontale Linie parallel zur x-Achse verläuft und sich immer auf einer konstanten Höhe befindet, sagen wir, dass diese Linien keinen Anstieg haben, also die Die Steigung dieser Geraden ist,
Somit ist Steigung = 0/Lauf = 0
Daraus wird geschlossen, dass die Steigung der horizontalen Linie Null ist.
Eine horizontale Linie zeichnen
Mit den unten beschriebenen Schritten lassen sich ganz einfach horizontale Linien zeichnen:
Schritt 1: Nehmen Sie einen Punkt auf der kartesischen Ebene, für den wir die horizontale Linie finden müssen. Angenommen, der Punkt ist (1, 2)
Schritt 2: Markiert die Y-Koordinate des Punktes. In diesem Fall ist die y-Koordinate 2.
Schritt 3: Markieren Sie andere Punkte, deren y-Koordinate mit dem Punkt in Schritt 1 übereinstimmt. Die anderen Punkte seien (-2, 2), (0, 2) und (7, 2).
Schritt 4: Verbinde alle Punkte zu einem Liniensegment und verlängere sie auf beiden Seiten, um eine horizontale Linie zu erhalten.
Dies ist die erforderliche horizontale Linie, die durch den Punkt (1, 2) verläuft und eine Steigung von Null hat.

Horizontale Liniengleichung
Wir wissen, dass die Gleichung der Linie im zweidimensionalen Koordinatensystem lautet:
y = mx + c
Wo,
- m ist die Steigung der Geraden
- c ist der Achsenabschnitt auf der y-Achse
Wir wissen, dass die Steigung der horizontalen Linie Null ist. Wenn wir diesen Wert in die obige Gleichung einsetzen, erhalten wir die Gleichung der horizontalen Linie:
y = 0x + c
Java-Reverse-Stringy = c
Wo C ist eine Konstante.
Somit ist die obige Gleichung y = c die Gleichung der horizontalen Linie.
Diese Gleichung bedeutet, dass die horizontale Linie eine Linie ist, die durch alle Punkte im Kartesischen verläuft, bei denen die y-Koordinate gleich „c“ ist. Dieser Linienschnitt hat keine x-Koordinate und daher schneidet diese Linie niemals die x-Achse und schneidet die y-Achse am Punkt (0, c).
Somit können wir sagen, dass die Gleichung der horizontalen Linie lautet: y = c(konstant) und sie durch den Punkt (a, c) verläuft, wo a jeden Wert annehmen kann und c immer konstant ist.
Horizontaler Linientest
Ein Test, der verwendet wird, um zu definieren, ob eine Funktion eine Eins-zu-eins-Funktion ist oder nicht, ist der Horizontallinientest. Beim horizontalen Linientest zeichnen wir eine horizontale Linie, die durch einen beliebigen Punkt der Funktion verläuft. Wenn die Linien die Funktion an einem anderen Punkt schneiden, ist die Funktion KEINE Eins-zu-eins-Funktion. Damit eine Funktion eins zu eins ist, muss sie den Horizontallinientest bestehen, d. h. jede horizontale Linie darf die Funktion nur einmal schneiden.
Wir wissen, dass Eins-zu-eins-Funktionen die Funktionen sind, bei denen wir für jeden Wert von x nur einen Wert von y haben. Wenn also die horizontale Linie durch die Funktion verläuft und sie nur einmal schneidet, können wir sagen, dass wir für den eindeutigen Wert von y einen eindeutigen Wert von x haben. Wenn die horizontale Linie die Funktion jedoch mehr als einmal schneidet, erhalten wir zwei Werte für den eindeutigen Wert von y, was bei der Eins-zu-eins-Funktion nicht der Fall ist.
Mithilfe des horizontalen Linientests können wir feststellen, ob eine Funktion eine Eins-Eins-Funktion ist. Dies kann anhand des unten hinzugefügten Bildes verstanden werden.

Im ersten Bild ist die Funktion eins zu eins, da die horizontale Linie nur durch einen Punkt der Funktion verläuft.
Im zweiten Bild ist die Funktion NICHT eins zu eins, da die horizontale Linie durch mehr als einen Punkt der Funktion verläuft.
Horizontale und vertikale Linien
Horizontale Linien sind Linien, die parallel zum Boden oder Horizont verlaufen. Diese Linien werden auch Schlaflinien genannt. Im kartesischen System verlaufen diese Linien parallel zur x-Achse, während es sich bei den vertikalen Linien um Linien handelt, die senkrecht zu den horizontalen Linien stehen und als stehende Linien bezeichnet werden. und sind parallel zur y-Achse im kartesischen System.
Horizontale Linien sind die Linien, die im kartesischen System von links nach rechts verlaufen, während vertikale Linien die Linien sind, die im kartesischen System auf und ab verlaufen.
Vertikale und horizontale Linien stehen senkrecht zueinander. Das unten hinzugefügte Bild zeigt eine vertikale und eine horizontale Linie.

Unterschiede zwischen vertikalen und horizontalen Linien
Die Unterschiede zwischen vertikalen und horizontalen Linien lassen sich anhand der unten angefügten Tabelle leicht verstehen.
| Horizontale Linie | Vertikale Linie |
|---|---|
| Diese Linien verlaufen parallel zum Boden oder zum Horizont. | Diese Zeilen sind aufrecht zum Boden oder zum Horizont. |
| Die Steigung der horizontalen Linie ist Null. | Die Steigung der vertikalen Linie ist undefiniert. |
| Die horizontale Linie bildete mit dem Horizont einen Winkel von null Grad. | Die vertikale Linie bildete mit dem Horizont einen Winkel von 90 Grad. |
| Die Gleichung der horizontalen Linie, die durch den Punkt (h, k) verläuft, lautet: y = k | Die Gleichung der vertikalen Linie, die durch den Punkt (h, k) verläuft, lautet: x = h |
| Horizontale Linien verlaufen im kartesischen System parallel zur x-Achse. | Vertikale Linien verlaufen im kartesischen System parallel zur y-Achse. |
| Beispiele für die Darstellung der horizontalen Linien sind:
| Beispiele für die Darstellung der vertikalen Linien sind:
|
Kurze Anmerkung zur horizontalen Linie
Eine horizontale Linie in der Mathematik ist vollkommen eben und parallel zum Horizont. Sie verläuft von links nach rechts und hat eine Steigung von 0. In der Geometrie wird sie als gerade Linie dargestellt, die zwei beliebige Punkte auf gleicher Höhe auf einer Ebene verbindet. Die Gleichung für eine horizontale Linie hat die Form (y = k), wobei (k) ein konstanter Wert ist, der die Höhe der Linie auf der y-Achse darstellt.
Mehr lesen:
- Arten von Linien
- Parallele Linien
- Wie füge ich in HTML eine horizontale Linie hinzu?
- Wie verwende ich den vollständigen horizontalen Zeilenabstand in HTML?
- So zeichnen Sie horizontale und vertikale Linien in einer Android-App mithilfe von XML
Beispiele für horizontale Linien
Beispiel 1: Finden Sie die Gleichung der horizontalen Linie, die durch den Punkt (1, -1) verläuft.
Lösung:
Wir wissen, dass die Steigung der horizontalen Linie m = 0 ist.
Gegebener Punkt (1, -1)
Gleichung der Geraden, die durch einen Punkt (x) verläuft1, Und1) und mit einer Steigung (m) ist,
und und1= m(x – x1)
Wenn wir die Werte in die obige Gleichung einsetzen, erhalten wir:
y – (-1) = 0(x – 1)
und + 1 = 0
y = -1
NullpointerExceptionSomit lautet die Gleichung der horizontalen Linie, die durch den Punkt (1, -1) verläuft, y = -1
Beispiel 2: Finden Sie die Gleichung der horizontalen Linie, die durch den Punkt (5, 9) verläuft.
Lösung:
Wir wissen, dass die Steigung der horizontalen Linie m = 0 ist.
Gegebener Punkt (5, 9)
Gleichung der Geraden, die durch einen Punkt (x) verläuft1, Und1) und mit einer Steigung (m) ist,
und und1= m(x – x1)
Wenn wir die Werte in die obige Gleichung einsetzen, erhalten wir:
y – (9) = 0(x – 5)
und – 9 = 0
y = 9
Somit lautet die Gleichung der horizontalen Linie, die durch den Punkt (5, 9) verläuft, y = 9
Beispiel 3: Finden Sie die Gleichung der horizontalen Linie, wenn der y-Achsenabschnitt der Linie 5 ist.
Lösung:
Die Gleichung der horizontalen Linie lautet:
y = k
Wo k ist y-Achsenabschnitt
Gegeben
- k = 5
Gleichung der horizontalen Linie,
y = 5
Somit lautet die Gleichung der horizontalen Linie mit dem y-Achsenabschnitt 5: y = 5
Beispiel 4: Finden Sie die Gleichung der horizontalen Linie, wenn der y-Achsenabschnitt der Linie -11/3 beträgt.
Lösung:
Die Gleichung der horizontalen Linie lautet:
y = k
Wo k ist y-Achsenabschnitt
Gegeben
- k = -11/3
Gleichung der horizontalen Linie,
y = -11/3
3y = -11
3 Jahre + 11 = 0
Somit lautet die Gleichung der horizontalen Linie mit dem y-Achsenabschnitt von -11/3: 3y + 11 = 0
Horizontale Linien – FAQs
Was sind horizontale Linien?
Horizontale Linien sind Linien, die parallel zum Horizont oder zum Boden verlaufen. Im kartesischen System verlaufen horizontale Linien parallel zur x-Achse.
Wie lautet die Gleichung der horizontalen Linie?
Die Gleichung der horizontalen Linie lautet:
ReactJS-Kartey = k
Wo k ist der Achsenabschnitt auf der y-Achse.
Wie groß ist die Steigung einer horizontalen Linie?
Die Steigung der horizontalen Linie ist immer gleich Null, da sie mit der x-Achse einen Winkel von null Grad bilden.
Was sind Beispiele für horizontale Linien?
Beispiele für die Darstellung der horizontalen Linien sind:
- Gerade Straße
- Unterseite der Treppe
- Basis einer beliebigen Figur usw.
Wie heißen die horizontalen Linien auf dem Globus?
Horizontale Linien, die auf dem Globus verlaufen, werden Breitengrade genannt und verlaufen parallel zum Äquator.
Welche Eigenschaften haben horizontale Linien?
Verschiedene Eigenschaften der horizontalen Linien sind:
- Sie verlaufen parallel zum Boden, zum Horizont und zur x-Achse.
- Sie stehen senkrecht zur y-Achse.
- Die Steigung der horizontalen Linie ist Null usw.
Welche Linie ist vertikal und horizontal?
Eine vertikale Linie verläuft parallel zur y-Achse und verläuft in einer Koordinatenebene gerade nach oben und unten, während eine horizontale Linie parallel zur x-Achse verläuft und gerade nach links und rechts verläuft.
Wie groß ist die Steigung einer horizontalen und vertikalen Linie?
Die Steigung einer Linie gibt deren Steilheit und Richtung an. Sie wird als Verhältnis der vertikalen Änderung zur horizontalen Änderung zwischen zwei Punkten auf der Linie berechnet.
Was sind die horizontalen und vertikalen Punktlinien?
Horizontale Linien erstrecken sich von links nach rechts oder von rechts nach links und verlaufen parallel zur x-Achse, während vertikale Linien nach oben und unten verlaufen und parallel zur y-Achse verlaufen. Diese beiden Arten von Linien stehen senkrecht zueinander.
