Der arithmetische Wert, der zur Darstellung der Menge und zur Durchführung von Berechnungen verwendet wird, wird als Zahlen definiert. Ein Symbol wie 4, 5, 6, das eine Zahl darstellt, wird als Zahl bezeichnet. Ohne Zahlen können wir keine Dinge, kein Datum, keine Uhrzeit, kein Geld usw. zählen. Diese Zahlen werden auch zur Messung und Kennzeichnung verwendet.

Aufgrund ihrer Eigenschaften sind Zahlen hilfreich bei der Durchführung arithmetischer Operationen. Diese Zahlen können in numerischer Form und auch in Worten geschrieben werden.

Zum Beispiel , 3 wird in Worten als drei geschrieben, 35 wird in Worten als fünfunddreißig geschrieben usw. Schüler können die Zahlen von 1 bis 100 in Worten schreiben, um mehr zu lernen.

Es gibt verschiedene Arten von Zahlen, die wir lernen können. Es handelt sich um ganze und natürliche Zahlen, ungerade und gerade Zahlen, rationale und irrationale Zahlen usw.

Was ist ein Zahlensystem?

Ein Zahlensystem ist eine Methode zur Darstellung von Zahlen durch Schreiben. Dabei handelt es sich um eine mathematische Methode zur Darstellung der Zahlen einer bestimmten Menge, indem die Zahlen oder Symbole auf mathematische Weise verwendet werden. Das Schriftsystem zur logischen Bezeichnung von Zahlen mithilfe von Ziffern oder Symbolen wird als Zahlensystem definiert.

Wir können die Ziffern von 0 bis 9 verwenden, um alle Zahlen zu bilden. Mit diesen Ziffern kann jeder unendliche Zahlen erstellen.

Zum Beispiel 156, 3907, 3456, 1298, 784859 usw.

Was ist eine Quadratwurzel?

Der Wert einer Anzahl von Quadratwurzeln, der bei Multiplikation mit sich selbst die ursprüngliche Zahl ergibt. Angenommen, a ist die Quadratwurzel von b, dann wird sie als a = √b dargestellt, oder wir können die gleiche Gleichung als a2 = b ausdrücken. Hier wird „√“, dieses Symbol, das wir zur Darstellung der Wurzel von Zahlen verwendet haben, als Radikal bezeichnet. Wenn die positive Zahl mit sich selbst multipliziert wird, stellt sie das Quadrat der Zahl dar. Die Quadratwurzel des Quadrats einer beliebigen positiven Zahl ergibt die ursprüngliche Zahl.

Zum Beispiel, Das Quadrat von 4 ist 16, 4²= 16 und die Quadratwurzel von 16, √16 = 4. Da 4 ein perfektes Quadrat ist, ist es einfach, die Quadratwurzel solcher Zahlen zu finden, aber für ein unvollständiges Quadrat ist es wirklich schwierig.

Quadratwurzel wird dargestellt als '√' Es wird als radikales Symbol bezeichnet. Um eine Zahl „a“ als Quadratwurzel darzustellen, kann dieses Symbol wie folgt geschrieben werden: „√a“, wobei a die Zahl ist.

Rujira Banerjee

Die Zahl hier unter dem Radikalsymbol wird Radikanden genannt. Beispielsweise wird die Quadratwurzel von 4 auch als Wurzel von 4 dargestellt. Beide stellen den gleichen Wert dar.

Die Formel zum Finden der Quadratwurzel lautet: a = √b

Eigenschaften von Quadratwurzeln

Sie ist als eine Eins-zu-Eins-Funktion definiert, die eine positive Zahl als Eingabe verwendet und die Quadratwurzel der gegebenen Eingabezahl zurückgibt.

Java ist gleich

f(x) = √x

Wenn hier beispielsweise x = 9 ist, gibt die Funktion den Ausgabewert als 3 zurück.

Die Eigenschaften der Quadratwurzel sind wie folgt:

• Wenn eine Zahl eine perfekte Quadratzahl ist, dann gibt es definitiv eine perfekte Quadratwurzel.
• Wenn eine Zahl mit einer geraden Anzahl von Nullen (0en) endet, können wir eine Quadratwurzel bilden.
• Die beiden Quadratwurzelwerte können multipliziert werden. Beispielsweise kann √3 mit √2 multipliziert werden, dann ist das Ergebnis √6.
• Wenn zwei gleiche Quadratwurzeln multipliziert werden, muss das Ergebnis eine Wurzelzahl sein. Es zeigt, dass das Ergebnis eine Nicht-Quadratwurzel-Zahl ist. Wenn beispielsweise √7 mit √7 multipliziert wird, ist das Ergebnis 7.
• Die Quadratwurzel negativer Zahlen ist undefiniert. Daher kann das perfekte Quadrat nicht negativ sein.
• Einige der Zahlen enden mit 2, 3, 7 oder 8 (in der Einerziffer), dann existiert die perfekte Quadratwurzel nicht.
• Einige der Zahlen enden mit 1, 4, 5, 6 oder 9 in der Einerstelle, dann hat die Zahl eine Quadratwurzel.

Es ist einfach, die Quadratwurzel einer Zahl zu finden, die ein perfektes Quadrat ist.

Perfekte Quadrate sind jene positiven Zahlen, die als Multiplikation einer Zahl mit sich selbst geschrieben werden können, oder man kann sagen, dass ein perfektes Quadrat eine Zahl ist, die dem Wert der Potenz 2 einer beliebigen ganzen Zahl entspricht.

Die Zahl, die als Produkt zweier gleicher Ganzzahlen ausgedrückt werden kann. Zum Beispiel ist 16 ein perfektes Quadrat, weil es das Produkt zweier gleicher ganzer Zahlen ist, 4 × 4 = 16. Allerdings ist 24 kein perfektes Quadrat, weil es nicht als Produkt zweier gleicher ganzer Zahlen ausgedrückt werden kann. (8 × 3 = 24).

Die Zahl, die man durch Quadrieren einer ganzen Zahl erhält, wird als perfektes Quadrat bezeichnet.

Wenn wir annehmen, dass N ein perfektes Quadrat einer ganzen Zahl y ist, kann dies als N = das Produkt von y und y = y geschrieben werden².

Zeichenfolge in char Java

Die perfekte Quadratformel kann also wie folgt ausgedrückt werden:

N = Y ²

Verwenden wir die Formel mit Werten:

Wenn y = 9 und N = y²

Das bedeutet, N = 9²= 81.

Hier ist 81 ein perfektes Quadrat von 9, weil es das Quadrat einer ganzen Zahl ist.

Mit Hilfe von Quadratwurzeln können wir feststellen, ob eine Zahl ein perfektes Quadrat ist oder nicht, indem wir die Quadratwurzel der gegebenen Zahl berechnen.

Wenn die Quadratwurzel eine ganze Zahl ist, ist die gegebene Zahl ein perfektes Quadrat, und wenn der Quadratwurzelwert keine ganze Zahl ist, dann ist die gegebene Zahl kein perfektes Quadrat.

Zum Beispiel, Um zu überprüfen, ob 24 ein perfektes Quadrat ist oder nicht, berechnen wir seine Quadratwurzel. √24 = 4,898979. Wie wir sehen können, ist 4,898979 keine ganze Zahl, also ist 24 kein perfektes Quadrat.

Nehmen wir ein anderes Beispiel

Die Zahl 49. √49 = 7. Wir können sehen, dass 7 eine ganze Zahl ist, also ist 49 ein perfektes Quadrat.

Zusammenführungssortierung Java

Ist 196 ein perfektes Quadrat?

Lösung:

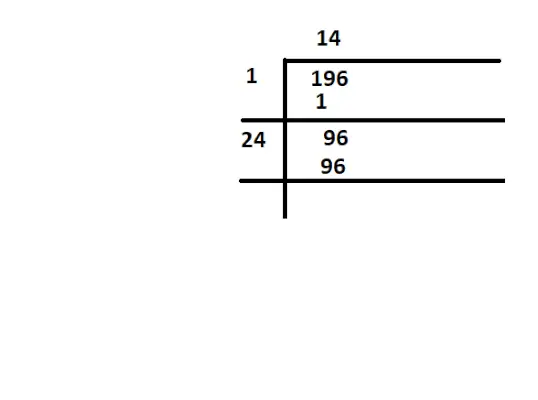
Um zu überprüfen, ob 196 ein perfektes Quadrat ist, müssen wir die Quadratwurzeln von 196 ermitteln

perfektes Quadrat von 196

Hier ist die Quadratwurzel von 196 14

Perfekte Quadrate sind jene positiven Zahlen, die als Multiplikation einer Zahl mit sich selbst geschrieben werden können, oder man kann sagen, dass ein perfektes Quadrat eine Zahl ist, die dem Wert der Potenz 2 einer beliebigen ganzen Zahl entspricht.

Hier können wir √196 = 14 oder 14 schreiben²= 14 × 14 = 196.

Daher ist 196 ein perfektes Quadrat.

Ähnliche Fragen

Frage 1: Was ist die Quadratwurzel von 625?

Lösung:

perfektes Quadrat von 625

Ameise gegen Maven

hier ist 625 das perfekte Quadrat von 25

Wir können also schreiben als √625 = 25 oder 25²= 25 × 25 = 625

Frage 2: Wie findet man die Quadratwurzel aus 24?

Lösung:

Quadratwurzel von 24

Hier ist 24 kein perfektes Quadrat von 4,8989.

daher √24 = 4,8989..

Frage 3: Finden Sie die Quadratwurzel von 361?

Lösung:

Quadrat von 361

Hier ist die Quadratwurzel von 361 19 , eine ganze Zahl, die ein perfektes Quadrat ist

Daher ist √361 = 19 oder 19²= 19 × 19 = 361