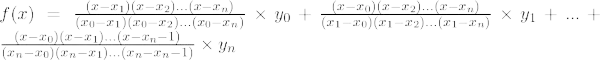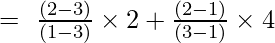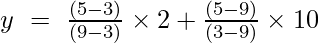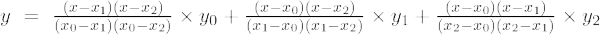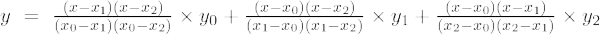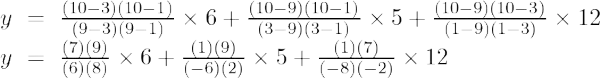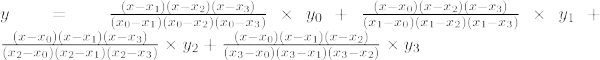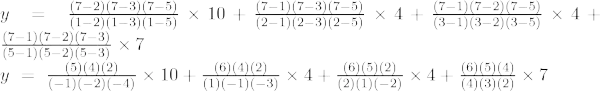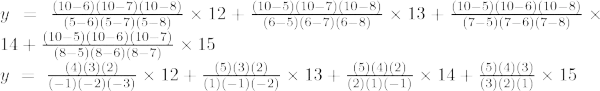logo

TechCodeview

Lagrange-Interpolationsformel

Lagrange-Interpolationsformel findet ein Polynom namens Lagrange-Polynom, das an einem beliebigen Punkt bestimmte Werte annimmt. Es ist ein n-ter Grad Polynomausdruck der Funktion f(x). Die Interpolationsmethode wird verwendet, um die neuen Datenpunkte innerhalb des Bereichs einer diskreten Menge bekannter Datenpunkte zu finden.

In diesem Artikel lernen wir die Lagrange-Interpolation, die Lagrange-Interpolationsformel, den Beweis für die Lagrange-Interpolationsformel, Beispiele basierend auf der Lagrange-Interpolationsformel und andere im Detail kennen.



Was ist Lagrange-Interpolation?

Die Lagrange-Interpolation ist eine Methode, den Wert einer Funktion an einem bestimmten Punkt zu ermitteln, wenn die Funktion nicht gegeben ist. Wir verwenden andere Punkte der Funktion, um den Wert der Funktion an jedem erforderlichen Punkt zu erhalten.

Angenommen, wir haben eine Funktion y = f(x), in der das Ersetzen der Werte von x unterschiedliche Werte von y ergibt. Und wir erhalten zwei Punkte (x1, Und1) und (x2, Und2) auf der Kurve wird dann der Wert von y bei x = a(Konstante) mithilfe der Lagrange-Interpolationsformel berechnet.

Lagrange-Interpolationsformel

Gegeben sind nur wenige reelle Werte x1, X2, X3, …, XNAndy1, Und2, Und3, …, UndNund es wird ein Polynom P mit reellen Koeffizienten geben, die die Bedingungen P(x) erfüllenich) = undich, ∀ i = {1, 2, 3, …, n} und der Grad des Polynoms P muss kleiner sein als die Anzahl der reellen Werte, d. h. Grad(P)



Lagrange-Interpolationsformel für n-te Ordnung

Die Lagrange-Interpolationsformel für nThDas Gradpolynom ist unten angegeben:

Lagrange-Interpolationsformel für das n Th Ordnung ist,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Lagrange-Interpolationsformel erster Ordnung

Wenn die Der Grad des Polynoms ist 1, dann wird es Polynom erster Ordnung genannt. Lagrange-Interpolationsformel für 1stOrdnungspolynome ist,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

char in Integer-Java umwandeln

Lagrange-Interpolationsformel zweiter Ordnung

Wenn der Grad des Polynoms 2 ist, wird es Polynom zweiter Ordnung genannt. Die Lagrange-Interpolationsformel für Polynome 2. Ordnung lautet:

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Beweis des Lagrange-Theorems

Betrachten wir ein Polynom n-ten Grades der gegebenen Form:

f(x) = A0(x – x1)(x – x2)(x – x3)…(x – xN) + A1(x – x1)(x – x2)(x – x3)…(x – xN) + … + A(n-1)(x – x1)(x – x2)(x – x3)…(x – xN)

Ersatzbeobachtungen xichum A zu bekommenich

Setzen Sie x = x0dann bekommen wir A0

f(x0) = und0= A0(X0- X1)(X0- X2)(X0- X3)…(X0- XN)

A 0 = und 0 /(X 0 - X 1 )(X 0 - X 2 )(X 0 - X 3 )…(X 0 - X N )

Durch Ersetzen von x = x1wir bekommen A1

f(x1) = und1= A1(X1- X0)(X1- X2)(X1- X3)…(X1- XN)

A 1 = und 1 /(X 1 - X 0 )(X 1 - X 2 )(X 1 - X 3 )…(X 1 - X N )

Ebenso durch Ersetzen von x = xNwir bekommen AN

f(xN) = undN= AN(XN- X0)(XN- X1)(XN- X2)…(XN- Xn-1)

A N = und N /(X N - X 0 )(X N - X 1 )(X N - X 2 )…(X N - X n-1 )

Wenn wir alle Werte von A ersetzenichin der Funktion f(x) mit i = 1, 2, 3, …n dann erhalten wir die Lagrange-Interpolationsformel als:

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} mal y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Eigenschaften der Lagrange-Interpolationsformel

Im Folgenden werden verschiedene Eigenschaften der Lagrange-Interpolationsformel besprochen:

  • Diese Formel wird verwendet, um den Wert der Funktion an jedem Punkt zu ermitteln, auch wenn die Funktion selbst nicht gegeben ist.
  • Es wird auch dann verwendet, wenn die angegebenen Punkte nicht gleichmäßig verteilt sind.
  • Es gibt den Wert der abhängigen Variablen für jede unabhängige Variable an, die zu einer beliebigen Funktion gehört, und wird daher in der numerischen Analyse zum Ermitteln der Werte der Funktion usw. verwendet.

Verwendung der Lagrange-Interpolationsformel

Im Folgenden werden verschiedene Anwendungen der Lagrange-Interpolationsformel erläutert.

  • Es wird verwendet, um den Wert der abhängigen Variablen bei einer bestimmten unabhängigen Variablen zu ermitteln, auch wenn die Funktion selbst nicht angegeben ist.
  • Es wird bei der Bildskalierung verwendet.
  • Es wird in der KI-Modellierung verwendet.
  • Es wird zum Unterrichten von NLPs usw. verwendet.

Mehr lesen,

  • Interpolationsformel
  • Lineare Interpolationsformel

Beispiele für die Verwendung der Lagrange-Interpolationsformel

Schauen wir uns einige Beispielfragen zur Lagrange-Interpolationsformel an.

Beispiel 1: Finden Sie den Wert von y bei x = 2 für die gegebene Menge von Punkten (1, 2),(3, 4)

Lösung:

Gegeben,

  • (X0, Und0) = (1, 2)
  • (X1, Und1) = (3, 4)

Die Lagrange-Interpolationsformel erster Ordnung lautet:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Bei x = 2

Und =~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Der Wert von y bei x = 2 beträgt 3

Beispiel 2: Ermitteln Sie den Wert von y bei x = 5 für die gegebene Menge von Punkten (9, 2), (3, 10).

Lösung:

Python oder

Gegeben,

  • (X0, Und0) = (9, 2)
  • (X1, Und1) = (3, 10)

Die Lagrange-Interpolationsformel erster Ordnung lautet:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Bei x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Der Wert von y bei x = 5 beträgt 7,33

Beispiel 3: Ermitteln Sie den Wert von y bei x = 1 für die gegebene Menge von Punkten (1, 6), (3, 4), (2, 5).

Lösung:

Gegeben,

  • (X0, Und0) = (1, 6)
  • (X1, Und1) = (3, 4)
  • (X2, Und2) = (2, 5)

Die Lagrange-Interpolationsformel zweiter Ordnung lautet:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Bei x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} imes 4+frac{(1-1)(1-3)}{(2-1)(2-3)} imes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)} imes 5

y = (12/2) + 0 + 0

y = 6

Der Wert von y bei x = 1 beträgt 6

Beispiel 4: Ermitteln Sie den Wert von y bei x = 10 für die gegebene Menge von Punkten (9, 6), (3, 5), (1, 12).

Jahr in Quartale

Lösung:

Gegeben,

  • (X0, Und0) = (9, 6)
  • (X1, Und1) = (3, 5)
  • (X2, Und2) = (1, 12)

Die Lagrange-Interpolationsformel zweiter Ordnung lautet:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Bei x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)} imes 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Der Wert von y bei x = 10 beträgt 9,375

Beispiel 5: Ermitteln Sie den Wert von y bei x = 7 für die gegebene Menge von Punkten (1, 10), (2, 4), (3, 4), (5, 7).

Lösung:

Gegeben,

  • (X0, Und0) = (1, 10)
  • (X1, Und1) = (2, 4)
  • (X2, Und2) = (3, 4)
  • (X3, Und3) = (5, 7)

Die Lagrange-Interpolationsformel dritter Ordnung lautet:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} imes y_3

Bei x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)} imes 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)} imes 4+frac{(6)(5)(4)}{(4)(3)(2)} imes 7

y = -50 + 64 – 60 + 35

Entfernen Sie den NPM-Cache

y = 99 – 110 = -elf

Der Wert von y bei x = 7 beträgt -11

Beispiel 6: Ermitteln Sie den Wert von y bei x = 10 für die gegebene Menge von Punkten (5, 12), (6, 13), (7, 14), (8, 15).

Lösung:

Gegeben,

  • (X0, Und0) = (5, 12)
  • (X1, Und1) = (6, 13)
  • (X2, Und2) = (7, 14)
  • (X3, Und3) = (8, 15)

Die Lagrange-Interpolationsformel dritter Ordnung lautet:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)} imes y_3

Bei x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15

y = -48 + 195 – 280 + 150

y = 17

Der Wert von y bei x = 10 beträgt 17

Beispiel 7: Finden Sie den Wert von y bei x = 0 für die gegebene Menge von Punkten (-2, 5),(1, 7)

Lösung:

Gegeben,

  • (X0, Und0) = (-2, 5)
  • (X1, Und1) = (1, 7)

Die Lagrange-Interpolationsformel erster Ordnung lautet:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Bei x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Der Wert von y bei x = 0 beträgt 6,33

Entwurfsmuster für die Fabrikmethode

FAQs zur Lagrange-Interpolationsformel

1. Was ist die Lagrange-Interpolationsformel?

Die Lagrange-Interpolationsformel ist eine Formel, die verwendet wird, um den Wert der abhängigen Variablen der Funktion für jede unabhängige Variable zu ermitteln, auch wenn die Funktion selbst nicht gegeben ist.

2. Was sind die Anwendungen der Lagrange-Interpolationsformel?

Die Lagranges-Formel findet vielfältige Anwendung in der modernen Mathematik und den Datenwissenschaften.

  • Es wird zur KI-Modellierung von Traning verwendet.
  • Es wird in der Bildverarbeitung verwendet.
  • Es wird zur grafischen Darstellung von 3D- und höheren Kurven usw. verwendet.

3. Was ist die Lagrange-Interpolationsformel erster Ordnung?

Die Lagranges-Interpolationsformel erster Ordnung lautet:

f(x) = (x – x 1 )/(X 0 - X 1 )×f 0 + (x – x 0 )/(X 1 - X 0 )×f 1

4. Was ist die Lagrange-Interpolationsformel zweiter Ordnung?

Die Lagranges-Interpolationsformel zweiter Ordnung lautet:

f(x) = [(x – x 1 )(x – x 2 )/(X 0 - X 1 )(X 0 - X 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(X 1 - X 0 )(X 1 - X 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(X 2 - X 0 )(X 2 - X 2 )]×f 0