Weniger als gleich ist ein Ungleichheitskonzept, das bedeutet, dass der Term auf der linken Seite der Ungleichung nicht größer sein darf als der Term auf der rechten Seite, d. h. der linke Term muss kleiner oder maximal gleich dem rechten Term sein. Der Artikel behandelt das Konzept „kleiner als oder gleich“ in der Mathematik und stellt das Symbol ≤ und seine Darstellung auf einer Zahlengeraden vor. Es enthält eine Tabelle mit mathematischen Symbolen, Übungsaufgaben und Antworten auf häufig gestellte Fragen zu Ungleichungen.
Inhaltsverzeichnis
Java-Druck
- Kleiner als gleich Vorzeichen
- Symbol „Kleiner als oder gleich“.
- Kleiner oder gleich auf einer Zahlengeraden
- Symbolnotationen von Ungleichungen
- Kleiner als gleich und größer als gleich
Kleiner als gleich Vorzeichen
Das Kleiner-gleich-Zeichen wird im Bild unten hinzugefügt,
Was ist kleiner oder gleich?
Kleiner oder gleich bedeutet, dass eine Sache nicht mehr als eine andere ist oder gleich sein kann. Wenn wir zum Beispiel 2x – 3 ≤ 9 haben, bedeutet das, dass 2 mal eine Zahl (x) minus 3 nicht mehr als 9 ist. Vereinfacht gesagt, wenn wir auf beiden Seiten 3 addieren, erhalten wir 2x ≤ 12. Dann durch Division Wenn wir beide Seiten mit 2 multiplizieren, finden wir x ≤ 6. Es heißt also, dass die Zahl (x) 6 oder weniger sein kann, und das ist immer noch wahr.
Überprüfen Sie auch
- Weniger als Symbol
- Gleichheitszeichen
Weniger als gleich dem Beispiel
Nehmen wir an, John und Peter sind zwei Freunde und John ist kleiner oder genauso alt wie Peter. Das bedeutet, dass Johannes entweder jünger oder genauso alt ist wie Petrus. Mit anderen Worten: Wir können sagen, dass Petrus entweder älter oder mindestens so alt wie Johannes ist.
Nehmen wir nun an, Johns Alter beträgt x Jahre und das von Peter „y“ Jahre, dann können wir dies in der Form der Gleichung „Kleiner als gleich“ wie folgt schreiben:
x ≤ y
Wo,
- x ist Johns Alter
- y ist Peters Zeitalter
Symbol „Kleiner als oder gleich“.
Symbol für kleiner oder gleich. ist ≤
In der Mathematik wird es verwendet, um zwei Größen zu vergleichen. Wenn Sie insbesondere a ≤ b sehen, bedeutet dies, dass a entweder kleiner oder gleich b ist. Dieses Symbol kombiniert die Idee von kleiner als (<) und gleich (=). Dies bedeutet also, dass der Wert auf der linken Seite des Symbols entweder kleiner oder gleich dem Wert auf der rechten Seite ist. Dies hilft dabei, Beziehungen zwischen Zahlen oder mathematischen Ausdrücken auszudrücken, bei denen eine kleiner als die andere oder gleich ihr sein kann.
Kleiner oder gleich auf einer Zahlengeraden
Das Konzept „kleiner oder gleich“ auf einer Zahlengeraden ist ein grundlegender mathematischer Ausdruck, der zum Vergleichen numerischer Werte verwendet wird. In diesem Zusammenhang bedeutet es, dass eine bestimmte Zahl entweder kleiner oder gleich einer anderen Zahl ist. Bei der Darstellung dieser Beziehung auf einer Zahlengeraden wird ein geschlossener Kreis (●) auf den Punkt gelegt, der dem kleineren oder gleichen Wert entspricht. Beispielsweise wird x ≤ 2 auf dem Zahlenstrahl wie folgt dargestellt
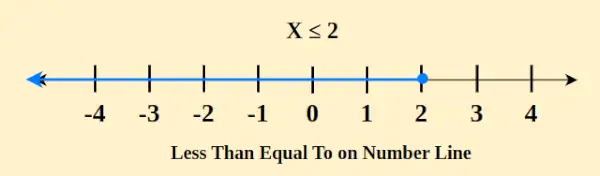
Zusätzlich verläuft von diesem Punkt aus eine Linie nach rechts, die alle Zahlen umfasst, die größer oder gleich dem angegebenen Wert sind. Die Einbeziehung eines geschlossenen Kreises dient dazu, hervorzuheben, dass der Endpunkt Teil des Vergleichs ist. Zur Veranschaulichung: Wenn A ≤ B, kann Punkt A an oder links von Punkt B auf der Zahlenlinie positioniert werden, was anzeigt, dass A entweder kleiner oder gleich B ist, mit Einschluss der Möglichkeit, dass A gleich B ist. Diese visuelle Darstellung hilft beim Verständnis der relativen Größen der verglichenen Werte.
Symbolnotationen von Ungleichungen
Nachfolgend werden die verschiedenen verwendeten Ungleichheitszeichen und deren Beschreibung hinzugefügt:
| Notation von Ungleichungssymbolen | |
|---|---|
| Symbolbeschreibung | Symbolnotation |
| Größer als Zeichen | > |
| Kleiner als Zeichen | < |
| Gleichbedeutend mit Zeichen | = |
| Ungleich mit Vorzeichen | ≠ |
| Größer kleiner oder gleich | ≥ |
| Gleich oder kleiner als | ≤ |
Kleiner als gleich und größer als gleich
Der Vergleich zwischen „Größer als gleich“ und „Kleiner als gleich“ wird unten aufgeführt:
| Unterschied zwischen „größer als gleich“ und „kleiner als gleich“. | ||
|---|---|---|
| Aspekt | Größer als gleich | Weniger als gleich |
| Bedeutung | Gibt einen Wert an, der größer oder minimal gleich dem angegebenen Wert ist | Geben Sie den Wert an, der kleiner oder maximal gleich dem angegebenen Wert ist |
| Symbol | ≥ | ≤ |
| Beispiel | Das Alter des Widders ist größer als 10 Jahre ⇒ Alter des Widders ≥ 10 Schnelle Sortierung | Das Alter von Rohan beträgt weniger als 15 Jahre ⇒ Alter von Rohan ≤ 15 |
Verwandte Lektüren ,
- Größer als kleiner als
- Größer als oder gleich wie
- Ungleichheiten
Weniger als gleich – Beispiele
Beispiel 1. Lösen Sie die Ungleichung: 3x – 5 ≤ 10.
Lösung:
Beginnen Sie mit der Addition von 5 auf beiden Seiten:
3x ≤ 15
Dann dividiere durch 3: x ≤ 5
Die Lösung ist also x ≤ 5
Beispiel 2. Lösen Sie die Ungleichung: -2y + 7 ≤ 1.
Lösung:
Subtrahiere 7 von beiden Seiten: -2y ≤ -6
Teilen Sie durch -2 und denken Sie daran, das Ungleichheitszeichen umzukehren: y ≥ 3
Die Lösung ist y ≥ 3
Weniger als gleich – Übungsprobleme
Probieren Sie die folgenden Übungsaufgaben aus, die auf dem Konzept „Kleiner als gleich“ basieren
Q1. Lösen Sie die Ungleichung: 2y – 8 ist kleiner oder gleich 10.
Q2. Wenn m 6 und n 3 ist, bestimmen Sie, ob m im Quadrat minus 5 kleiner oder gleich 2n plus 1 ist.
Q3. Lösen Sie nach x auf: 3x plus 7 ist kleiner oder gleich 22.
Q4. Wenn q eine positive Zahl ist, sodass 4q minus 6 kleiner oder gleich 14 ist, ermitteln Sie die möglichen Werte für q.
F5. Bestimmen Sie den Wertebereich für a, der die Ungleichung 2a plus 5 erfüllt und kleiner oder gleich 15 ist.
Weniger als gleich – FAQs
1. Was ist kleiner oder gleich?
Kleiner oder gleich bezeichnet eine Beziehung zwischen zwei Werten, was bedeutet, dass der erste Wert entweder kleiner oder gleich dem zweiten ist.
2. Wie wird „Kleiner als“ oder „Gleich“ auf einer Zahlengeraden dargestellt?
Auf einer Zahlengerade wird diese Beziehung visuell dargestellt, indem ein geschlossener Kreis (●) auf der Zahl platziert wird, die dem kleineren oder gleichen Wert entspricht, und eine Linie nach rechts verlängert wird, die alle Zahlen umfasst, die größer oder gleich diesem Wert sind.
3. Was bedeutet ein geschlossener Kreis auf der Zahlengeraden?
Der geschlossene Kreis betont die Einbeziehung des Endpunkts in den Vergleich. Wenn beispielsweise A ≤ B, bedeutet dies, dass Punkt A entweder am oder links von Punkt B auf der Zahlengeraden liegt, einschließlich der Möglichkeit, dass A gleich B ist.
4. Was ist ein Beispiel für die Lösung einer Kleiner-gleich-Ungleichung?
Betrachten Sie die Ungleichung 2x – 3 ≤ 9. Wenn wir auf beiden Seiten 3 addieren, erhalten wir 2x ≤ 12. Dann finden wir durch Division beider Seiten durch 2 x ≤ 6. Daher ist die Lösung der Ungleichung x ≤ 6.
5. Wie löst man Ungleichungen, die kleiner oder gleich sind?
Um Ungleichungen wie ax + b ≤ c zu lösen, besteht der übliche Ansatz darin, die Ungleichung durch Addition, Subtraktion, Multiplikation oder Division zu manipulieren, um die Variable zu isolieren und den Wertebereich zu bestimmen, der die Ungleichung erfüllt.
6. Was ist das Symbol für „kleiner als gleich“ und „größer als gleich“?
Symbol für weniger als gleich ist ≤ während das Symbol für größer als gleich ist ≥.
