In der Informatik gibt es einige Probleme, deren Lösung noch nicht gefunden wurde. Die Probleme werden in sogenannte Klassen eingeteilt Komplexitätsklassen . In der Komplexitätstheorie ist eine Komplexitätsklasse eine Reihe von Problemen mit verwandter Komplexität. Diese Kurse helfen Wissenschaftlern, Probleme danach zu gruppieren, wie viel Zeit und Raum sie zur Lösung von Problemen und zur Überprüfung der Lösungen benötigen. Es ist der Zweig der Berechnungstheorie, der sich mit den Ressourcen befasst, die zur Lösung eines Problems erforderlich sind.
vb und vb net
Die gemeinsamen Ressourcen sind Zeit und Raum, also wie viel Zeit der Algorithmus benötigt, um ein Problem zu lösen, und die entsprechende Speichernutzung.
- Die Zeitkomplexität eines Algorithmus wird verwendet, um die Anzahl der Schritte zu beschreiben, die zur Lösung eines Problems erforderlich sind. Sie kann jedoch auch verwendet werden, um zu beschreiben, wie lange es dauert, die Antwort zu überprüfen.
- Die räumliche Komplexität eines Algorithmus beschreibt, wie viel Speicher für den Betrieb des Algorithmus erforderlich ist.
Komplexitätsklassen sind hilfreich bei der Organisation ähnlicher Problemtypen.
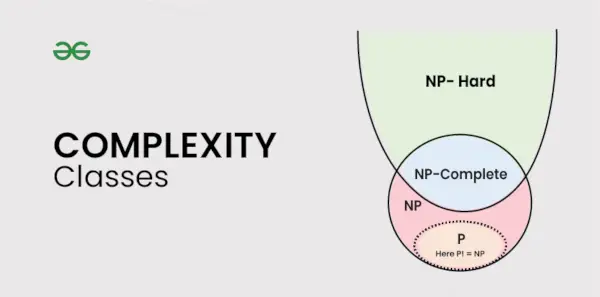
Arten von Komplexitätsklassen
In diesem Artikel werden die folgenden Komplexitätsklassen behandelt:
- P-Klasse
- NP-Klasse
- CoNP-Klasse
- NP-hart
- NP-vollständig
P-Klasse
Das P in der P-Klasse steht für Polynomzeit. Es handelt sich um eine Sammlung von Entscheidungsproblemen (Probleme mit einer Ja- oder Nein-Antwort), die von einer deterministischen Maschine in polynomieller Zeit gelöst werden können.
Merkmale:
- Die Lösung für P-Problem s ist leicht zu finden.
- P ist oft eine Klasse von Rechenproblemen, die lösbar und handhabbar sind. Praktikabel bedeutet, dass die Probleme sowohl in der Theorie als auch in der Praxis gelöst werden können. Aber die Probleme, die theoretisch, aber nicht in der Praxis gelöst werden können, werden als unlösbar bezeichnet.
Diese Klasse enthält viele Probleme:
- Berechnung des größten gemeinsamen Teilers.
- Finden einer maximalen Übereinstimmung.
- Zusammenführen, sortieren
NP-Klasse
Das NP in der NP-Klasse steht für Nichtdeterministische Polynomzeit . Dabei handelt es sich um die Sammlung von Entscheidungsproblemen, die von einer nichtdeterministischen Maschine in polynomieller Zeit gelöst werden können.
Merkmale:
- Die Lösungen der NP-Klasse sind schwer zu finden, da sie von einer nichtdeterministischen Maschine gelöst werden, aber die Lösungen sind leicht zu überprüfen.
- Probleme von NP können durch eine Turingmaschine in polynomieller Zeit verifiziert werden.
Beispiel:
öffentliches vs. privates Java
Betrachten wir ein Beispiel, um das besser zu verstehen NP-Klasse . Angenommen, es gibt ein Unternehmen mit insgesamt 1000 Mitarbeiter mit einzigartigem Mitarbeiter Ausweise . Gehen Sie davon aus, dass es welche gibt 200 ihnen zur Verfügung stehende Räume. Eine Auswahl von 200 Mitarbeiter müssen in Gruppen zusammengefasst werden, aber der CEO des Unternehmens verfügt über die Daten einiger Mitarbeiter, die aus persönlichen Gründen nicht im selben Raum arbeiten können.
Dies ist ein Beispiel für eine Z.B Problem. Da ist es einfach zu überprüfen, ob die gegebene Auswahl von 200 Die von einem Kollegen vorgeschlagene Anzahl der Mitarbeiter ist zufriedenstellend oder nicht, d. h. kein aus der Mitarbeiterliste entnommenes Paar erscheint auf der vom CEO bereitgestellten Liste. Die Erstellung einer solchen Liste von Grund auf scheint jedoch so schwierig zu sein, dass sie völlig unpraktisch ist.
Es bedeutet, dass wir, wenn uns jemand die Lösung des Problems liefern kann, das richtige und das falsche Paar in polynomieller Zeit finden können. Also für die Z.B Klassenproblem ist die Antwort möglich, die in polynomieller Zeit berechnet werden kann.
Diese Klasse enthält viele Probleme, die man effektiv lösen möchte:
- Boolesches Erfüllbarkeitsproblem (SAT).
- Hamilton-Pfad-Problem.
- Diagrammfärbung.
Co-NP-Klasse
Co-NP steht für das Komplement der NP-Klasse. Das heißt, wenn die Antwort auf ein Problem in Co-NP „Nein“ lautet, gibt es einen Beweis, der in polynomieller Zeit überprüft werden kann.
Merkmale:
Befehl im Knoten js
- Wenn ein Problem X in NP liegt, dann ist sein Komplement X‘ auch in CoNP.
- Für ein NP- und CoNP-Problem ist es nicht erforderlich, alle Antworten auf einmal in polynomieller Zeit zu verifizieren. Es besteht die Notwendigkeit, nur eine bestimmte Antwort mit Ja oder Nein in polynomieller Zeit zu verifizieren, damit ein Problem in NP oder CoNP liegt.
Einige Beispielprobleme für CoNP sind:
- Um Primzahlen zu überprüfen.
- Faktorisierung ganzer Zahlen.
NP-schwere Klasse
Ein NP-schweres Problem ist mindestens so schwer wie das schwierigste Problem in NP und es handelt sich um eine Klasse von Problemen, bei der jedes Problem in NP auf NP-schwer reduziert wird.
Merkmale:
- Alle NP-schweren Probleme liegen nicht in NP.
- Es dauert lange, sie zu überprüfen. Das heißt, wenn eine Lösung für ein NP-schweres Problem gegeben ist, dauert es lange, zu prüfen, ob sie richtig ist oder nicht.
- Ein Problem A ist NP-schwer, wenn es für jedes Problem L in NP eine polynomiale Zeitreduktion von L auf A gibt.
Einige Beispiele für Probleme in Np-hard sind:
- Halteproblem.
- Qualifizierte boolesche Formeln.
- Kein Hamilton-Zyklus.
NP-vollständige Klasse
Ein Problem ist NP-vollständig, wenn es sowohl NP als auch NP-schwer ist. NP-vollständige Probleme sind die schwierigen Probleme in NP.
Merkmale:
- NP-vollständige Probleme sind etwas Besonderes, da jedes Problem der NP-Klasse in polynomieller Zeit in NP-vollständige Probleme umgewandelt oder reduziert werden kann.
- Wenn man ein NP-vollständiges Problem in polynomieller Zeit lösen könnte, dann könnte man auch jedes NP-Problem in polynomieller Zeit lösen.
Einige Beispielprobleme sind:
- Hamilton-Zyklus.
- Befriedigungsfähigkeit.
- Scheitelpunktabdeckung .
| Komplexitätsklasse | Charakteristisches Merkmal |
| P | Leicht in polynomieller Zeit lösbar. |
| Z.B | Ja, Antworten können in polynomieller Zeit überprüft werden. |
| Co-NP | Nein, Antworten können in polynomieller Zeit überprüft werden. |
| NP-hart | Alle NP-schweren Probleme sind nicht in NP und es dauert lange, sie zu überprüfen. |
| NP-vollständig | Ein Problem, das NP und NP-schwer ist, ist NP-vollständig. |
