Eine rekursive Funktion kann als eine Routine definiert werden, die sich selbst direkt oder indirekt aufruft.

Mit anderen Worten: Eine rekursive Funktion ist eine Funktion, die ein Problem löst, indem sie kleinere Instanzen desselben Problems löst. Diese Technik wird in der Programmierung häufig verwendet, um Probleme zu lösen, die in einfachere, ähnliche Teilprobleme zerlegt werden können.

sonniges Deol

Bedarf an rekursiver Funktion:

Eine rekursive Funktion ist eine Funktion, die ein Problem löst, indem sie kleinere Instanzen desselben Problems löst. Diese Technik wird in der Programmierung häufig verwendet, um Probleme zu lösen, die in einfachere, ähnliche Teilprobleme zerlegt werden können.

1. Komplexe Aufgaben lösen:

Rekursive Funktionen zerlegen komplexe Probleme in kleinere Instanzen desselben Problems, was zu kompaktem und lesbarem Code führt.

2. Teile und herrsche:

Rekursive Funktionen eignen sich für Divide-and-Conquer-Algorithmen wie Merge-Sort und Quicksort, um Probleme in kleinere Teilprobleme zu zerlegen, sie rekursiv zu lösen und die Lösungen mit dem ursprünglichen Problem zusammenzuführen.

32-Bit-Architektur vs. 64-Bit

3. Zurückverfolgen :

Rekursives Backtracking ist ideal zum Erkunden und Lösen von Problemen wie N-Queens und Sudoku.

4. Dynamisch Programmierung:

Rekursive Funktionen lösen dynamische Programmierprobleme effizient, indem sie Teilprobleme lösen und ihre Lösungen zu einer Gesamtlösung kombinieren.

5. Baum und Graphstrukturen:

Rekursive Funktionen eignen sich hervorragend für die Arbeit mit Baum- und Diagrammstrukturen und vereinfachen Durchlauf- und Mustererkennungsaufgaben .

So schreiben Sie eine rekursive Funktion:

Komponenten einer rekursiven Funktion:

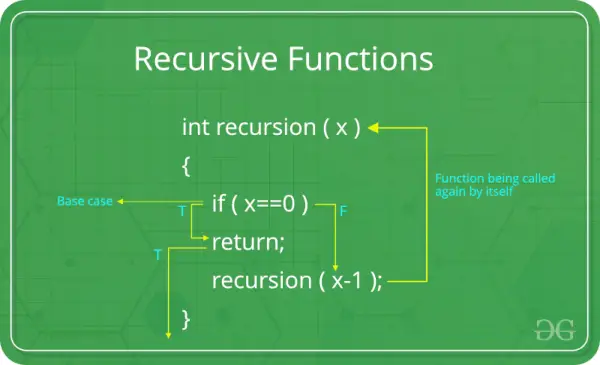
Basisfall: Jede rekursive Funktion muss einen Basisfall haben. Der Basisfall ist das einfachste Szenario, das keine weitere Rekursion erfordert. Dies ist eine Beendigungsbedingung, die verhindert, dass sich die Funktion auf unbestimmte Zeit selbst aufruft. Ohne einen geeigneten Basisfall kann eine rekursive Funktion zu einer unendlichen Rekursion führen.

Rekursiver Fall: Im rekursiven Fall ruft sich die Funktion mit den geänderten Argumenten selbst auf. Das ist die Essenz der Rekursion – die Lösung eines größeren Problems durch die Zerlegung in kleinere Instanzen desselben Problems. Der rekursive Fall sollte sich mit jeder Iteration dem Basisfall annähern.

Betrachten wir das Beispiel von Fakultät der Zahl :

In diesem Beispiel ist der Basisfall wann N Ist 0 , und die Funktion kehrt zurück 1 . Der rekursive Fall multipliziert N mit dem Ergebnis der mit Parameter aufgerufenen Funktion n – 1 . Der Prozess wird fortgesetzt, bis der Basisfall erreicht ist.

Centos vs. Redhat

Es muss unbedingt sichergestellt werden, dass die rekursive Funktion einen korrekten Basisfall hat und dass die rekursiven Aufrufe zum Basisfall führen. Andernfalls wird die Prozedur möglicherweise unbegrenzt ausgeführt, was zu einem Stapelüberlauf führt (der den für Funktionsaufrufe zugewiesenen verfügbaren Speicher überschreitet).

Unten ist die Implementierung der Fakultät einer Zahl:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Zeitkomplexität: An)
Hilfsraum: An)