Ein Set in der Python-Programmierung ist ein ungeordneter Sammlungsdatentyp, der iterierbar und veränderbar ist und keine doppelten Elemente enthält.
Mengen werden durch { } dargestellt (Werte in geschweiften Klammern eingeschlossen)
Der Hauptvorteil der Verwendung eines Sets im Gegensatz zu einem Liste besteht darin, dass es über eine hochoptimierte Methode zur Überprüfung verfügt, ob ein bestimmtes Element in der Menge enthalten ist. Dies basiert auf einer Datenstruktur, die als Hash-Tabelle bekannt ist. Da Mengen ungeordnet sind, können wir nicht wie in Listen über Indizes auf Elemente zugreifen.
Beispiel für Python-Sets
Python3
var>=> {>'Geeks'>,>'for'>,>'Geeks'>}> type>(var)> |
>
>
Ausgabe:
set>
Zeitkomplexität: O(1)
Hilfsraum: O(1)
Geben Sie Casting mit der Python-Set-Methode ein
Für die Typumwandlung wird die Python-Methode set() verwendet.
Python3
# typecasting list to set> myset>=> set>([>'a'>,>'b'>,>'c'>])> print>(myset)> # Adding element to the set> myset.add(>'d'>)> print>(myset)> |
>
>
Ausgabe:
Die Python-Menge ist ein ungeordneter Datentyp, was bedeutet, dass wir nicht wissen können, in welcher Reihenfolge die Elemente der Menge gespeichert sind.
{'c', 'b', 'a'} {'d', 'c', 'b', 'a'}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Überprüfen Sie mit Python Set die Einzigartigkeit und Unveränderlichkeit
Python-Sets dürfen keinen doppelten Wert haben und sobald sie erstellt wurden, können wir ihren Wert nicht ändern.
Python3
# Python program to demonstrate that> # a set cannot have duplicate values> # and we cannot change its items> # a set cannot have duplicate values> myset>=> {>'Geeks'>,>'for'>,>'Geeks'>}> print>(myset)> # values of a set cannot be changed> myset[>1>]>=> 'Hello'> print>(myset)> |
>
>
Ausgabe:
Der erste Code erklärt, dass die Menge keinen doppelten Wert haben kann. Jeder Gegenstand darin ist ein einzigartiger Wert.
Der zweite Code generiert einen Fehler, da wir nach der Erstellung des Satzes keinen Wert mehr zuweisen oder ändern können. Wir können nur Elemente im Set hinzufügen oder löschen.
{'Geeks', 'for'} TypeError: 'set' object does not support item assignment> Heterogenes Element mit Python-Set
Python-Sets können darin heterogene Elemente speichern, d. h. ein Set kann eine Mischung aus String-, Integer-, Booleschen- usw. Datentypen speichern.
Python3
# Python example demonstrate that a set> # can store heterogeneous elements> myset>=> {>'Geeks'>,>'for'>,>10>,>52.7>,>True>}> print>(myset)> |
>
json-Datei
>
Ausgabe:
{True, 10, 'Geeks', 52.7, 'for'}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Gefrorene Python-Sets
Gefrorene Sets In Python handelt es sich um unveränderliche Objekte, die nur Methoden und Operatoren unterstützen, die ein Ergebnis erzeugen, ohne die eingefrorene Menge oder Mengen zu beeinflussen, auf die sie angewendet werden. Dies kann mit der Methode Frozenset() in Python erfolgen.
Während Elemente einer Menge jederzeit geändert werden können, bleiben Elemente der eingefrorenen Menge nach der Erstellung gleich.
Wenn keine Parameter übergeben werden, wird ein leeres Frozenset zurückgegeben.
Python
# Python program to demonstrate differences> # between normal and frozen set> # Same as {'a', 'b','c'}> normal_set>=> set>([>'a'>,>'b'>,>'c'>])> print>(>'Normal Set'>)> print>(normal_set)> # A frozen set> frozen_set>=> frozenset>([>'e'>,>'f'>,>'g'>])> print>(>'
Frozen Set'>)> print>(frozen_set)> # Uncommenting below line would cause error as> # we are trying to add element to a frozen set> # frozen_set.add('h')> |
>
>
Ausgabe:
Normal Set {'a', 'c', 'b'} Frozen Set {'e', 'g', 'f'}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Interne Arbeitsweise von Set
Dies basiert auf einer Datenstruktur, die als Hash-Tabelle bekannt ist. Wenn an derselben Indexposition mehrere Werte vorhanden sind, wird der Wert an diese Indexposition angehängt, um eine verknüpfte Liste zu bilden.
In werden Python-Sets mithilfe eines Wörterbuchs mit Dummy-Variablen implementiert, wobei die Schlüsselelemente die Mitglieder sind, die mit größerer Optimierung der Zeitkomplexität festgelegt werden.
Set-Implementierung:
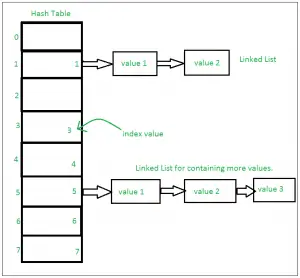
Sets mit zahlreichen Operationen auf einer einzelnen HashTable:
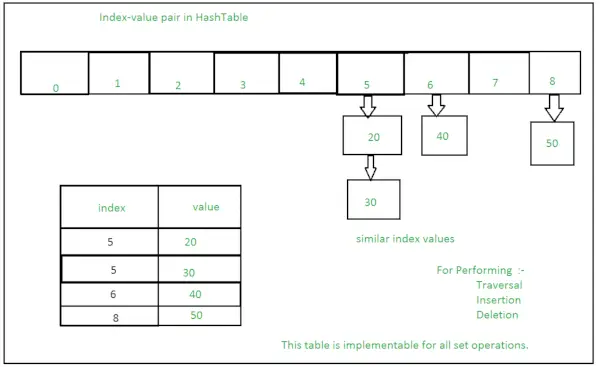
Methoden für Mengen
Elemente zu Python-Sets hinzufügen
Die Einfügung in das Set erfolgt durch set.add( )-Funktion, bei der ein geeigneter Datensatzwert zum Speichern in der Hash-Tabelle erstellt wird. Identisch mit der Suche nach einem Element, d. h. O(1) im Durchschnitt. Im schlimmsten Fall kann es jedoch dazu kommen An) .
Python3
# A Python program to> # demonstrate adding elements> # in a set> # Creating a Set> people>=> {>'Jay'>,>'Idrish'>,>'Archi'>}> print>(>'People:'>, end>=> ' '>)> print>(people)> # This will add Daxit> # in the set> people.add(>'Daxit'>)> # Adding elements to the> # set using iterator> for> i>in> range>(>1>,>6>):> >people.add(i)> print>(>'
Set after adding element:'>, end>=> ' '>)> print>(people)> |
>
>
Ausgabe:
People: {'Idrish', 'Archi', 'Jay'} Set after adding element: {1, 2, 3, 4, 5, 'Idrish', 'Archi', 'Jay', 'Daxit'}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Union-Operation für Python-Sets
Zwei Mengen können mit der Funktion union() oder | zusammengeführt werden Operator. Auf beide Hash-Tabellenwerte wird zugegriffen und sie werden mit einer Zusammenführungsoperation durchlaufen, um die Elemente zu kombinieren, gleichzeitig werden Duplikate entfernt. Die zeitliche Komplexität davon ist O(len(s1) + len(s2)) Dabei sind s1 und s2 zwei Mengen, deren Vereinigung durchgeführt werden muss.
Python3
# Python Program to> # demonstrate union of> # two sets> people>=> {>'Jay'>,>'Idrish'>,>'Archil'>}> vampires>=> {>'Karan'>,>'Arjun'>}> dracula>=> {>'Deepanshu'>,>'Raju'>}> # Union using union()> # function> population>=> people.union(vampires)> print>(>'Union using union() function'>)> print>(population)> # Union using '|'> # operator> population>=> people|dracula> print>(>'
Union using '|' operator'>)> print>(population)> |
>
>
Ausgabe:
Union using union() function {'Karan', 'Idrish', 'Jay', 'Arjun', 'Archil'} Union using '|' operator {'Deepanshu', 'Idrish', 'Jay', 'Raju', 'Archil'}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Schnittpunktoperation für Python-Sets
Dies kann über den Operator „intersection()“ oder „&“ erfolgen. Gemeinsame Elemente werden ausgewählt. Sie ähneln der Iteration über die Hash-Listen und der Kombination derselben Werte in beiden Tabellen. Die zeitliche Komplexität beträgt O(min(len(s1), len(s2)), wobei s1 und s2 zwei Mengen sind, deren Vereinigung durchgeführt werden muss.
Python3
# Python program to> # demonstrate intersection> # of two sets> set1>=> set>()> set2>=> set>()> for> i>in> range>(>5>):> >set1.add(i)> for> i>in> range>(>3>,>9>):> >set2.add(i)> # Intersection using> # intersection() function> set3>=> set1.intersection(set2)> print>(>'Intersection using intersection() function'>)> print>(set3)> # Intersection using> # '&' operator> set3>=> set1 & set2> print>(>'
Intersection using '&' operator'>)> print>(set3)> |
>
>
Ausgabe:
Intersection using intersection() function {3, 4} Intersection using '&' operator {3, 4}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Unterschiede zwischen Mengen in Python finden
Um Unterschiede zwischen Mengen zu finden. Ähnlich wie beim Finden von Unterschieden in der verknüpften Liste. Dies erfolgt über den Operator „different()“ oder „–“. Die zeitliche Komplexität beim Finden der Differenz s1 – s2 beträgt O(len(s1))
Python3
# Python program to> # demonstrate difference> # of two sets> set1>=> set>()> set2>=> set>()> for> i>in> range>(>5>):> >set1.add(i)> for> i>in> range>(>3>,>9>):> >set2.add(i)> # Difference of two sets> # using difference() function> set3>=> set1.difference(set2)> print>(>' Difference of two sets using difference() function'>)> print>(set3)> # Difference of two sets> # using '-' operator> set3>=> set1>-> set2> print>(>'
Difference of two sets using '-' operator'>)> print>(set3)> |
>
>
Ausgabe:
Difference of two sets using difference() function {0, 1, 2} Difference of two sets using '-' operator {0, 1, 2}> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Python-Sets löschen
Die Set Clear()-Methode leert den gesamten Satz an Ort und Stelle.
Python3
# Python program to> # demonstrate clearing> # of set> set1>=> {>1>,>2>,>3>,>4>,>5>,>6>}> print>(>'Initial set'>)> print>(set1)> # This method will remove> # all the elements of the set> set1.clear()> print>(>'
Set after using clear() function'>)> print>(set1)> |
>
>
Ausgabe:
Initial set {1, 2, 3, 4, 5, 6} Set after using clear() function set()> Zeitkomplexität: O(n)
Hilfsraum: O(n)
Es gibt jedoch zwei große Fallstricke bei Python-Sets:
- Das Set verwaltet Elemente nicht in einer bestimmten Reihenfolge.
- Einem Python-Set können nur Instanzen unveränderlicher Typen hinzugefügt werden.
Zeitkomplexität von Mengen
| Betrieb | Durchschnittlicher Fall | Schlimmsten Fall | Anmerkungen |
|---|---|---|---|
| x in s | O(1) | An) | |
| Union s|t | O(len(s)+len(t)) | ||
| Kreuzung s&t | O(min(len(s), len(t)) | O(len(s) * len(t)) | Ersetzen Sie min durch max, wenn t keine Menge ist |
| Mehrere Kreuzungen s1&s2&..&sn | (n-1)*O(l) wobei l max(len(s1),..,len(sn)) ist | ||
| Unterschied s-t | O(nur(s)) |
Operatoren für Mengen
Sets und eingefrorene Sets unterstützen die folgenden Operatoren:
| Betreiber | Anmerkungen |
|---|---|
| Geben Sie s ein | Eindämmungsprüfung |
| Schlüssel nicht in s | Nichteinschlussprüfung |
| s1 == s2 | s1 entspricht s2 |
| s1 != s2 | s1 ist nicht gleichbedeutend mit s2 |
| s1 <= s2 | s1 ist eine Teilmenge von s2 |
| s1 | s1 ist die echte Teilmenge von s2 |
| s1>= s2 | s1 ist eine Obermenge von s2 |
| s1> s2 | s1 ist die echte Obermenge von s2 |
| s1 | s2 | die Vereinigung von s1 und s2 |
| s1 & s2 | der Schnittpunkt von s1 und s2 |
| s1 – s2 | die Menge der Elemente in s1, aber nicht in s2 |
| s1 ˆ s2 | die Menge der Elemente in genau einem von s1 oder s2 |
Aktuelle Artikel zu Python Set.
stdin c-Programmierung
