Der Einheitskreis ist ein Kreis mit einem Radius von 1. Der Mittelpunkt des Einheitskreises liegt im Ursprung (0,0) auf der Achse. Der Umfang Der Einheitskreis beträgt 2π Einheiten, während die Fläche des Einheitskreises π Einheiten beträgt2. Es trägt alle Eigenschaften von Circle. Der Einheitskreis hat die Gleichung x2+ und2= 1. Dieser Einheitskreis hilft bei der Definition verschiedener trigonometrischer Konzepte.
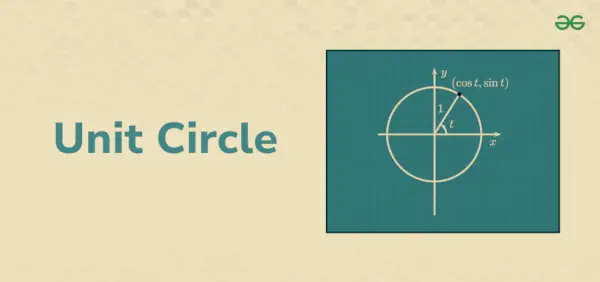
Einheitskreis
Der Einheitskreis wird oft als S bezeichnet1Die Verallgemeinerung auf höhere Dimensionen ist die Einheitssphäre. Lassen Sie uns weiter unten mehr über Einheitskreis, Formel und gelöste Beispiele im Detail erfahren.
Was ist der Einheitskreis?
Ein Einheitskreis ist ein Kreis mit einem Radius von einer (1) Einheit. Wir verwenden die kartesische Ebene, um einen Einheitskreis zu zeichnen, und ein Einheitskreis ist ein Polynom 2. Grades mit zwei Variablen. Der Einheitskreis hat verschiedene Anwendungen in der Trigonometrie und Algebra und wird hauptsächlich verwendet, um die Werte verschiedener trigonometrischer Verhältnisse wie sin x, cos x, tan x und andere zu ermitteln.
Einheitskreisdefinition
In der Mathematik definieren wir einen Einheitskreis als den Ort eines festen Punktes, der eine Einheit vom Mittelpunkt des Kreises entfernt ist. Ein Einheitskreis hat einen Radius von einer Einheit und daher der Name Einheitskreis.
Gleichung des Einheitskreises
Wir wissen, dass die Gleichung jedes Kreises mit Mittelpunkt (h, k) und Radius „r“ lautet:
(x – h) 2 + (y – k) 2 = r 2
Für einen Einheitskreis wissen wir, dass r 1 Einheit ist und daher lautet die Gleichung des Einheitskreises:
(x – h) 2 + (y – k) 2 = 1
Formel des Einheitskreises
Wenn der Mittelpunkt des Einheitskreises der Ursprung ist, d. h. (h, k) = (0, 0), dann lautet die Gleichung des Einheitskreises:
X 2 + und 2 = 1
Im unten hinzugefügten Bild ist ein Einheitskreis mit den Mittelpunktkoordinaten h und k dargestellt. Wenn der Kreis seinen Ursprung hat, ist der Wert von h und k Null und der Radius AP ist gleich 1 Einheit.
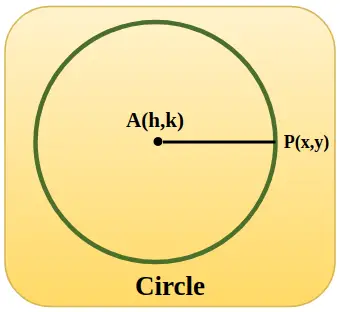
Trigonometrische Funktionen mit Einheitskreis
Die Anwendung des Satzes des Pythagoras auf einen Einheitskreis kann besser zum Verständnis trigonometrischer Funktionen genutzt werden. Dazu gehen wir davon aus, dass ein rechtwinkliges Dreieck innerhalb eines Einheitskreises in der kartesischen Koordinatenebene liegt. Beachten Sie, dass der Radius dieses Kreises die Hypotenuse des rechtwinkligen Dreiecks bezeichnet.
Der Radius des Kreises bildet einen Vektor. Dies führt zur Bildung eines Winkels, sagen wir θ, mit der positiven x-Achse. Nehmen wir an, dass x die Basislänge und y die Höhenlänge des rechtwinkligen Dreiecks ist. Außerdem sind die Koordinaten der Radiusvektor-Endpunkte jeweils (x, y).
Das rechtwinklige Dreieck hat jeweils die Seiten 1, x und y. Das trigonometrische Verhältnis kann nun wie folgt berechnet werden:
sin θ = Höhe/Hypotenuse = y/1
cos θ = Basis/Hypotenuse = x/1
Jetzt,
- Sünde θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Durch Ersetzen der Werte von θ können wir Hauptwerte aller trigonometrischen Funktionen erhalten. Ebenso werden Werte trigonometrischer Funktionen bei unterschiedlichen Werten gefunden.
Einheitskreis mit Sin Cos und Tan
Jeder Punkt auf dem Einheitskreis mit den Koordinaten (x, y) wird durch trigonometrische Identitäten als (cosθ, sinθ) dargestellt. Die Koordinaten der Radiusecken stellen den Kosinus und den Sinus der θ-Werte für einen bestimmten Wert von θ und der Radiuslinie dar. Es gilt cos θ = x und sin θ = y. Es gibt vier Teile eines Kreises, die jeweils in einem Quadranten liegen und einen Winkel von 90°, 180°, 270° und 360° bilden. Die Radiuswerte liegen jeweils zwischen -1 und 1. Außerdem liegen die Werte für sin θ und cos θ jeweils zwischen 1 und -1.
Einheitskreis und trigonometrische Identitäten
Die trigonometrischen Identitäten des Einheitskreises für Kotangens, Sekante und Kosekans können mithilfe der Identitäten für sin, cos und tan berechnet werden. Zusammenfassend erhalten wir ein rechtwinkliges Dreieck mit den Seiten 1, x und y. Die Berechnung der Einheitskreisidentitäten kann wie folgt ausgedrückt werden:
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- Sek. θ = 1/x
- cosec θ = 1/y
- Kinderbett θ = x/y
Einheitskreisdiagramm
Das Einheitskreisdiagramm ist ein Diagramm, das den Wert der trigonometrischen Funktion Sinus und Cosinus für verschiedene Winkel enthält. Das Einheitskreisdiagramm dafür ist unten hinzugefügt:
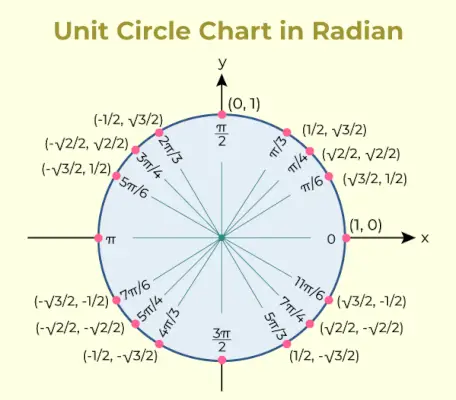
Einheitskreistisch
Die in der Einheitskreistabelle verwendeten trigonometrischen Verhältnisse werden verwendet, um die Koordinaten der Punkte auf dem Einheitskreis aufzulisten, die gemeinsamen Winkeln entsprechen.
| Winkel | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| ohne | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 Java konvertiert eine Ganzzahl in einen String | 0 |
| Also | 0 | 1/√(3) | 1 | √(3) | Nicht definiert |
| csc | Nicht definiert | 2 | √(2) | 23) | 1 |
| Sek | 1 | 23) | √(2) | 2 Minimax-Algorithmus | Nicht definiert |
| Kinderbett | Nicht definiert | √(3) | 1 | 1/√(3) | 0 |
Einheitskreis Pythagoräische Identitäten
Es gibt drei pythagoreische Identitäten und alle lassen sich leicht beweisen, indem man das Konzept des Einheitskreises verwendet, den die drei pythagoreischen Identitäten darstellen:
- ohne2θ + cos2θ = 1
- 1 + also2θ = Sek2ich
- 1 + Kinderbett2θ = cosec2ich
Komplexe Ebene des Einheitskreises
Komplexe Zahlen und komplexe Ebene lassen sich leicht mit dem Konzept des Einheitskreises erklären. Die Gleichung des Einheitskreises in komplexer Form lautet:
|z| = 1
ODER
X 2 + und 2 = 1
In der Euler-Form wird eine komplexe Zahl wie folgt dargestellt:
z = e Es = cos t + i(sin t)
Mehr lesen
Gelöste Beispiele zum Einheitskreis
Q1: Beweisen Sie, dass der Punkt Q auf einem Einheitskreis liegt, Q = [1/√(6), √4/√6]
Lösung:
Gegeben,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Die Gleichung des Einheitskreises lautet:
X2+ und2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
Links ≠ Rechts
Somit liegt der Punkt Q[1/√(6), √4/√6] nicht auf dem Einheitskreis.
F2: Berechnen Sie also 30 Ö unter Verwendung der Sinus- und Cosinus-Werte des Einheitskreises.
Lösung:
tan 30° unter Verwendung von Sinus- und Cos-Werten,
tan 30° = (sin 30°)/ (cos 30°)
- ohne 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
tan 30° = 1/√(3)
F3: Überprüfen Sie, ob der Punkt P [1/2, √(3)/2] auf dem Einheitskreis liegt.
Lösung:
Gegeben,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Die Gleichung des Einheitskreises lautet:
- X2+ und2= 1
Links
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Übungsfragen zum Unit Circle
Q1. Prüfen Sie, ob die Punkte A (1/2, 3/2) auf einem Einheitskreis liegen.
Q2. Prüfen Sie, ob die Punkte A (2, 1/2) auf einem Einheitskreis liegen.
Q3. Ermitteln Sie den Wert von cos 240°
Q4. Finden Sie den Wert von tan 320°
F5. Finden Sie den Wert von sin 160°
Unit Circle – FAQs
Was ist der Einheitskreis?
Ein Einheitskreis ist definiert als die Position eines Punktes, der eine Einheit von einem festen Punkt entfernt ist. Es hat einen Mittelpunkt bei (0,0) und der Wert seines Radius ist 1.
Wie kann man überprüfen, ob ein Punkt auf dem Einheitsreif liegt?
Jeder Punkt, der in einer zweidimensionalen Ebene liegt und die Form (x, y) hat, wird in die Einheitskreisgleichung x eingefügt2+ und2= 1, um zu überprüfen, ob es auf dem Kreis liegt oder nicht.
Wie lautet die Formel des Einheitskreises?
Die Einheitskreisformel ist eine Formel, die zur algebraischen Darstellung eines Einheitskreises verwendet wird. Die Einheitskreisformel lautet:
X 2 + und 2 = 1
Warum heißt es Einheitskreis?
Ein Einheitskreis wird Einheitskreis genannt, weil er einen Radius von einer (1) Einheit hat.
