Trigonometrietabelle ist eine Standardtabelle, die uns hilft, die Werte trigonometrischer Verhältnisse für Standardwinkel wie 0°, 30°, 45°, 60° und 90° zu ermitteln. Es besteht aus allen sechs trigonometrischen Verhältnissen: Sinus, Cosinus, Tangens, Kosekans, Sekante und Kotangens.
Lassen Sie uns die Trigonometrietabelle im Detail kennenlernen.
Inhaltsverzeichnis
- Trigonometrietabelle
- Tabelle der trigonometrischen Funktionen
- Trick, um trigonometrische Verhältnisse zu lernen
- So merken Sie sich die trigonometrische Tabelle
- So erstellen Sie eine Triggertabelle
- Trigonometrische Formeln
- Tabelle der trigonometrischen Identitäten
- Beispiele für trigonometrische Tabellen
Trigonometrietabelle
Eine trigonometrische Tabelle ist die Anordnung der Werte aller sechs trigonometrischen Funktionen für ihre gemeinsamen Winkel in tabellarischer Form.
Notiz – Trigonometrie ist ein Teilgebiet der Mathematik, das sich mit den Beziehungen zwischen den Winkeln und Seiten rechtwinkliger Dreiecke beschäftigt.
Tabelle der trigonometrischen Funktionen
Die Trigonometrie hat 6 grundlegende trigonometrische Funktionen: Sinus, Kosinus, Tangens, Kosekant, Sekant und Kotangens. Schauen wir uns nun die trigonometrischen Funktionen an.
Für jedes rechtwinklige Dreieck mit Senkrechter (P), Basis (B) und Hypotenuse (H) lauten die sechs trigonometrischen Funktionen wie folgt:
| Tabelle der trigonometrischen Funktionen | |||
| Funktion | Definition | Darstellung | Beziehung zu Seiten eines rechtwinkligen Dreiecks |
| Sein | Verhältnis von Senkrechter und Hypotenuse | ohne ich | Gegenseite / Hypotenuse |
| Kosinus | Verhältnis von Basis und Hypotenuse | cos ich | Ankathete / Hypotenuse |
| Tangente | Verhältnis von Sinus und Cosinus eines Winkels | Also ich | Gegenseite / Angrenzende Seite |
| Kosekans | Kehrwert von sin θ | csc ich oder cosec ich | Hypotenuse / Gegenseite |
| Sekante | Kehrwert von cos θ | Sek ich | Hypotenuse / Ankathete |
| Kotangens | Kehrwert von tan θ | Kinderbett ich | Angrenzende Seite / Gegenseite |
Notiz – Trigonometrie ist ein Zweig der Mathematik, der sich mit den Beziehungen zwischen den Winkeln und Seiten von Dreiecken, insbesondere rechtwinkligen Dreiecken, befasst. Dabei geht es um das Studium und die Anwendung von Sinus-, Kosinus-, Tangens- und anderen trigonometrischen Funktionen zur Lösung von Problemen in verschiedenen Bereichen.
Überprüfen : Trigonometrie: Formeln, Tabelle, Identitäten und Verhältnisse
Trick, um trigonometrische Verhältnisse zu lernen
Studieren Sie die unten besprochene Tabelle, um die trigonometrischen Verhältnisse auf leicht zu merkende Weise zu lernen.
String in int umwandeln
| Manche Menschen haben lockiges schwarzes Haar, um Schönheit zu erzeugen |
| sin θ (Einige) = Senkrecht (Menschen) / Hypotenuse (haben) |
| cos θ (lockig) = Basis (schwarz) / Hypotenuse (Haar) |
| tan θ (zu) = Senkrecht (produzieren) / Basis (Schönheit) |
So merken Sie sich die trigonometrische Tabelle
Wenn Sie alle Trigonometrieformeln kennen, können Sie sich die Trigonometrietabelle ganz einfach merken. Es gibt auch einen Trick namens Einhandtrick um sich die Trigonometrietabelle zu merken.

Schritt 1: Zählen Sie in der Abbildung oben für die Sinustabelle die Finger auf der linken Seite für den Standardwinkel.
Schritt 2: Teilen Sie die Anzahl der Finger auf der linken Seite (im 1. Schritt berechnen) durch 4
Schritt 3: Finden Sie die Quadratwurzel des in Schritt 2 berechneten Werts.
Überprüfen: Trigonometrieformeln – Liste aller trigonometrischen Identitäten und Formeln
So erstellen Sie eine Triggertabelle
Studieren Sie die folgenden Schritte, um die trigonometrische Tabelle für Standardwinkel zu erstellen.
Schritt 1: Erstellen Sie die Tabelle
Erstellen Sie eine Tabelle und listen Sie alle Winkel auf, z 0°, 30°, 45°, 60° und 90°, in der obersten Reihe. Geben Sie alle trigonometrischen Funktionen sin, cos, tan, cosec, sec und cot in die erste Spalte ein.
Schritt 2: Bewerten Sie den Wert für alle Winkel der Sinusfunktion.
Um die Werte der Sinusfunktion zu ermitteln, dividieren Sie 0, 1, 2, 3 und 4 durch 4 und ziehen Sie jeweils die Wurzel aus jedem Wert als:
Denn der Wert von sin 0° = √(0/4) = 0
Ähnlich,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| ohne 0° | ohne 30° | ohne 45° | ohne 60° | ohne 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Schritt 3: Bewerten Sie den Wert für alle Winkel der Cos-Funktion
Der Wert der cos-Funktion ist das Gegenteil des Wertes der sin-Funktion, d. h. cos 0° = sin 90°, cos 30° = sin 60° und cos 45° = sin 45°, also
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Schritt 4: Bewerten Sie den Wert für alle Winkel der Tan-Funktion
Der Wert der tan-Funktion ist gleich der sin-Funktion dividiert durch die cos-Funktion, d. h. tan x = sin x / cos x. Der Wert aller Winkel in der Tan-Funktion wird wie folgt berechnet:
tan 0°= sin 0° / cos 0° = 0/1 = 0, ähnlich
| also 0° | also 30° | also 45° | also 60° | also 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Nicht definiert |
Schritt 5: Bewerten Sie den Wert für alle Winkel der Cosec-Funktion
Vereinigte Staaten, wie viele Städte
Der Wert der cosec-Funktion ist gleich dem Kehrwert der sin-Funktion. Der Wert von cosec 0° wird durch Bildung des Kehrwerts von sin 0° ermittelt
cosec 0° = 1 / sin 0° = 1 / 0 = Nicht definiert. Ähnlich,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Nicht definiert | 2 | √2 | 23 | 1 |
Schritt 6: Bewerten Sie den Wert für alle Winkel der Sek-Funktion
Der Wert der sec-Funktion ist gleich dem Kehrwert der cos-Funktion. Der Wert von sec 0° wird durch Bildung des Kehrwerts von cos 0° ermittelt
sec 0° = 1 / cos 0° = 1 / 1 = 1. Ebenso gilt:
| Sek. 0° | Sek. 30° | Sek. 45° | Sek. 60° | Sek. 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Nicht definiert |
Schritt 7: Bewerten Sie den Wert für alle Winkel der Cot-Funktion
Der Wert der cot-Funktion ist gleich dem Kehrwert der tan-Funktion. Der Wert von cot 0° wird durch Bildung des Kehrwerts von tan 0° ermittelt
cot 0° = 1 /tan 0° = 1 / 0 = Nicht definiert. Ähnlich,
| Kinderbett 0° | Kinderbett 30° | Kinderbett 45° | Kinderbett 60° | Kinderbett 90° |
|---|---|---|---|---|
| Nicht definiert | √3 | 1 | 1/√3 | 0 |
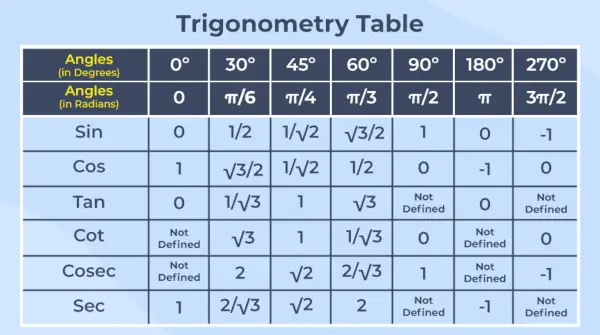
Auf diese Weise können wir die folgende Tabelle der trigonometrischen Verhältnisse erstellen:
| Trigonometrische Tabelle mit Grad und Bogenmaß | |||||||
|---|---|---|---|---|---|---|---|
| Winkel (in Grad) | Winkel (im Bogenmaß) | Ohne | Cos | Also | Cosec | Sek | Kinderbett |
| 0° | 0 | 0 | 1 | 0 | Nicht definiert | 1 | Nicht definiert |
| 30° | S. 6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | S./4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | S./3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Nicht definiert | 1 | Nicht definiert | 0 |
Trigonometrische Formeln
Lassen Sie uns etwas über einige trigonometrische Formeln im Zusammenhang mit Komplementär- und Ergänzungswinkeln lernen.
- Ergänzende Winkel: Winkelpaar, dessen Summe 90° beträgt
- Ergänzungswinkel: Winkelpaar, dessen Summe 180° beträgt
Überprüfen: Trigonometrische Verhältnisse
Trigonometrische Identitäten komplementärer Winkel
Die Identitäten komplementärer Winkel basieren auf der Beziehung zwischen den trigonometrischen Funktionen zweier Winkel, deren Summe 90 Grad (oder π/2 Bogenmaß) ergibt. Diese werden als bezeichnet kofunktionale Identitäten .
| Trigonometrische Funktion | Identität |
|---|---|
| Sein | sin(90°− ich )=cos ich |
| Kosinus | cos(90°− ich )=ohne ich |
| Tangente | tan(90°− ich )=Kinderbett ich |
| Kotangens | Kinderbett(90°− ich )=so ich |
| Sekante | sec(90°− ich )=csc ich |
| Kosekans | cosec(90°− ich )=Sek ich |
Trigonometrische Identitäten ergänzender Winkel
Die Identitäten ergänzender Winkel beziehen sich auf die trigonometrischen Funktionen zweier Winkel, die sich zu 180 Grad (oder π Bogenmaß) summieren.
| Trigonometrische Funktion | Identität |
|---|---|
| Sein | sin(180°− ich )=ohne ich |
| Kosinus | cos(180°− ich )=−cos ich |
| Tangente | tan(180°− ich )=−tan ich |
| Kotangens | Kinderbett(180°− ich )=−cot ich |
| Sekante | sec(180°− ich )=−sek ich |
| Kosekans | cosec(180°− ich )=cosec ich |
Tabelle der trigonometrischen Identitäten
Trigonometrische Identitäten sind die Identitäten, die häufig zur Lösung trigonometrischer Probleme verwendet werden. Es gibt verschiedene trigonometrische Identitäten, aber die drei wichtigsten trigonometrischen Identitäten sind:
| Tabelle der trigonometrischen Identitäten | |
| Trigonometrische Identität | Formel |
| Pythagoräische Identität | ohne2θ + cos2θ = 1 |
| Sekanten-Tangenten-Identität | Sek2θ – also2θ = 1 |
| Kosekans-Kotangens-Identität | cosec2θ – Kinderbett2θ = 1 |
Überprüfen Sie außerdem:
- Trigonometrische Verhältnisse
- Inverse trigonometrische Identitäten
- Höhen und Entfernungen
Beispiele für trigonometrische Tabellen
Lassen Sie uns einige Fragen zur trigonometrischen Tabelle lösen.
Beispiel 1: Wenn sin θ = 4/5, dann finden Sie alle trigonometrischen Werte.
Lösung:
Hier haben wir,
Sünde θ = 4/5
as, sin θ = Senkrecht / Hypotenuse
also haben wir Senkrechte (P)= 4 und Hypotenuse(H) = 5
Also nach dem Satz des Pythagoras H 2 = P 2 +B 2
Lassen Sie uns den Wert der Basis (B) herausfinden.
52= B2+ 42
25 = B2+ 16
25 -16 = B2
B2= 9
B = 3Jetzt haben wir,
Sin θ = Senkrecht/Hypotenuse
= AB/AC = 4/5Java system.out.printlnKosinus θ = Basis/Hypotenuse
= BC/AC = 3/5Tangente θ = Senkrecht/Basis
= AB/BC = 4/3Kosekans θ = Hypotenuse/Senkrechte
= AC/AB = 5/4Sekante θ = Hypotenuse/Basis
= AC/BC = 5/3Kotangens θ = Basis/Senkrechte
= BC/AB = 3/4
Beispiel 2: Ermitteln Sie den Wert von cos 45° + 2 sin 60° – tan 60°.
Lösung:
Aus der Trigonometrietabelle:
cos 45° = 1/√2, sin 60° = √3/2 und tan 60° = √3
Daher,
cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Beispiel 3: Ermitteln Sie den Wert von cos 75°.
Lösung:
Wir wissen das,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Fazit – Trigonometrietabelle
Die Trigonometrietabelle Bietet eine umfassende Referenz für die trigonometrischen Funktionen Sinus, Cosinus, Tangens, Kosekans, Sekante und Kotangens sowie ihre jeweiligen Werte für verschiedene Winkel. ICH Es dient als wertvolles Werkzeug zur Lösung trigonometrische Gleichungen, Analyse geometrischer Beziehungen und Verständnis des Verhaltens periodischer Phänomene. Ob in In Mathematik, Physik, Ingenieurwesen oder anderen Bereichen hilft die Trigonometrietabelle bei Berechnungen, Problemlösungen und Visualisierung und trägt zu einem tieferen Verständnis trigonometrischer Konzepte und ihrer Anwendungen in realen Szenarien bei.
ASCII-Tabelle Java
Trigonometrietabelle – FAQs
Was ist Trigonometrie?
Trigonometrie ist der Zweig der Mathematik, der sich mit Winkeln und Seiten jedes Dreiecks befasst.
Was ist eine trigonometrische Tabelle?
Eine Trigonometrietabelle ist eine Tabelle, die die Werte aller sechs trigonometrischen Funktionen für die gemeinsamen Winkel enthält.
Wer hat die Trigonometrietabelle erfunden?
Der griechische Astronom Hipparchos (127 v. Chr.) erfand die Trigonometrietabelle.
Was sind Standardwinkel in einer trigonometrischen Tabelle?
Die Standardwinkel in einer trigonometrischen Tabelle sind 0°, 30°, 45°, 60° und 90°
Was ist der Wert von tan 45 Grad?
Der Wert von tan 45 Grad beträgt 1.
Wie lerne ich die Trigonometrietabelle?
Der Trick beim Erlernen der trigonometrischen Tabelle ist:
- Sie müssen alle Werte aller Winkel der Sinusfunktion lernen.
- Der Wert aller Winkel der Cos-Funktion ist das Spiegelbild der Sin-Funktion.
- Die Werte der Tan-Funktion können berechnet werden, indem die Sin-Funktion durch die Cos-Funktion dividiert wird.
- Der Wert der cosec-Funktion ist der Kehrwert von sin.
- Ebenso sind sec und cot reziprok zur cos- und cot-Funktion.
Was sind sechs Grundfunktionen in der trigonometrischen Tabelle?
Die sechs grundlegenden trigonometrischen Funktionen in der trigonometrischen Tabelle sind Sinus, Kosinus, Tangens, Sekant, Kotangens und Kosekans.
Gibt es Taschenrechner, die Trigonometrietabellen ersetzen können?
Wissenschaftliche Taschenrechner können trigonometrische Verhältnisse für jeden Winkel berechnen8.
Wozu dient eine Trigonometrietabelle?
Die Trigonometrietabelle wird grundsätzlich verwendet, um die Werte aller trigonometrischen Verhältnisse für alle Winkel zu ermitteln. Diese Werte haben eine Reihe realer Anwendungen.
