BINÄRER HEAP – TECHCODEVIEW.COM - IT-PROBLEME UND LÖSUNGEN

A Binärer Heap ist ein Kompletter Binärbaum Dies wird zum effizienten Speichern von Daten verwendet, um das maximale oder minimale Element basierend auf seiner Struktur abzurufen.

Ein binärer Heap ist entweder Min Heap oder Max Heap. In einem Min-Binär-Heap muss der Schlüssel am Stamm das Minimum aller im Binär-Heap vorhandenen Schlüssel sein. Die gleiche Eigenschaft muss für alle Knoten im Binärbaum rekursiv wahr sein. Max Binary Heap ähnelt MinHeap.

Beispiele für Min Heap:

10 10
/ /
20 100 15 30
/ / /
30 40 50 100 40

Wie wird Binary Heap dargestellt?

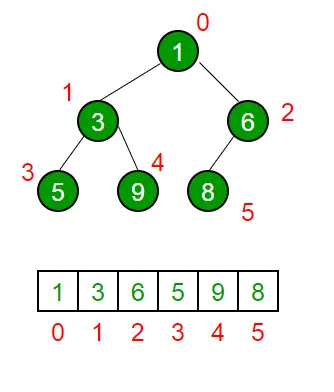
Ein binärer Heap ist ein Kompletter Binärbaum . Ein binärer Heap wird normalerweise als Array dargestellt.

Das Wurzelelement befindet sich bei Arr[0].
Die folgende Tabelle zeigt Indizes anderer Knoten für das i^ThKnoten, d. h. Arr[i]:

Arr[(i-1)/2]	Gibt den übergeordneten Knoten zurück
Arr[(2*i)+1]	Gibt den linken untergeordneten Knoten zurück
Arr[(2*i)+2]	Gibt den rechten untergeordneten Knoten zurück

Die zur Erzielung einer Array-Darstellung verwendete Traversierungsmethode ist Level-Order-Traversal . Bitte beziehen Sie sich auf Array-Darstellung des binären Heaps für Details.

Binärer Heap-Baum

Operationen auf Heap:

Nachfolgend sind einige Standardoperationen für den Min-Heap aufgeführt:

getMin(): Es gibt das Wurzelelement von Min Heap zurück. Die zeitliche Komplexität dieser Operation beträgt O(1) . Im Falle eines Maxheaps wäre es so getMax() .
extractMin() : Entfernt das minimale Element aus MinHeap. Die zeitliche Komplexität dieser Operation beträgt O(log N) da dieser Vorgang die Heap-Eigenschaft beibehalten muss (durch Aufruf von heapify() ) nach dem Entfernen der Wurzel.
verringernKey() : Verringert den Wert des Schlüssels. Die zeitliche Komplexität dieser Operation beträgt O(log N) . Wenn der verringerte Schlüsselwert eines Knotens größer ist als der des übergeordneten Knotens, müssen wir nichts tun. Andernfalls müssen wir nach oben gehen, um die verletzte Heap-Eigenschaft zu beheben.
einfügen() : Das Einsetzen eines neuen Schlüssels dauert O(log N) Zeit. Wir fügen am Ende des Baums einen neuen Schlüssel hinzu. Wenn der neue Schlüssel größer als sein übergeordneter Schlüssel ist, müssen wir nichts tun. Andernfalls müssen wir nach oben gehen, um die verletzte Heap-Eigenschaft zu beheben.
löschen() : Das Löschen eines Schlüssels dauert ebenfalls O(log N) Zeit. Wir ersetzen den zu löschenden Schlüssel durch den minimalen Unendlichen durch Aufruf verringernKey() . Nach verringerter Key () muss der Minus-Unendlich-Wert die Wurzel erreichen, also rufen wir auf extractMin() um den Schlüssel abzuziehen.

Nachfolgend finden Sie die Implementierung grundlegender Heap-Operationen.

C++

// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>

'
Overflow: Could not insertKey
'>

;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest != i)   {   swap(&harr[i], &harr[smallest]);   MinHeapify(smallest);   }  }    // A utility function to swap two elements  void swap(int *x, int *y)  {   int temp = *x;   *x = *y;   *y = temp;  }    // Driver program to test above functions  int main()  {   MinHeap h(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   cout << h.extractMin() << ' ';   cout << h.getMin() << ' ';   h.decreaseKey(2, 1);   cout << h.getMin();   return 0;  }>

Was ist ein Hashset in Java?

Java

// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0>

&& heapArray[i]   swap(heapArray, i, parent(i));   i = parent(i);   }   return true;   }     // Decreases value of given key to new_val.   // It is assumed that new_val is smaller   // than heapArray[key].   public void decreaseKey(int key, int new_val) {   heapArray[key] = new_val;     while (key != 0 && heapArray[key]   swap(heapArray, key, parent(key));   key = parent(key);   }   }     // Returns the minimum key (key at   // root) from min heap   public int getMin() {   return heapArray[0];   }       // Method to remove minimum element   // (or root) from min heap   public int extractMin() {   if (current_heap_size <= 0) {   return Integer.MAX_VALUE;   }     if (current_heap_size == 1) {   current_heap_size--;   return heapArray[0];   }     // Store the minimum value,   // and remove it from heap   int root = heapArray[0];     heapArray[0] = heapArray[current_heap_size - 1];   current_heap_size--;   MinHeapify(0);     return root;   }     // This function deletes key at the   // given index. It first reduced value   // to minus infinite, then calls extractMin()   public void deleteKey(int key) {   decreaseKey(key, Integer.MIN_VALUE);   extractMin();   }     // A recursive method to heapify a subtree   // with the root at given index   // This method assumes that the subtrees   // are already heapified   private void MinHeapify(int key) {   int l = left(key);   int r = right(key);     int smallest = key;   if (l   smallest = l;   }   if (r   smallest = r;   }     if (smallest != key) {   swap(heapArray, key, smallest);   MinHeapify(smallest);   }   }     // Increases value of given key to new_val.   // It is assumed that new_val is greater   // than heapArray[key].   // Heapify from the given key   public void increaseKey(int key, int new_val) {   heapArray[key] = new_val;   MinHeapify(key);   }     // Changes value on a key   public void changeValueOnAKey(int key, int new_val) {   if (heapArray[key] == new_val) {   return;   }   if (heapArray[key]   increaseKey(key, new_val);   } else {   decreaseKey(key, new_val);   }   }  }    // Driver Code  class MinHeapTest {   public static void main(String[] args) {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   System.out.print(h.extractMin() + ' ');   System.out.print(h.getMin() + ' ');     h.decreaseKey(2, 1);   System.out.print(h.getMin());   }  }    // This code is contributed by rishabmalhdijo>

Python

Java in Array auflisten

# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>self>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if>

(l   heapArray[l]   {   smallest = l;   }   if (r   heapArray[r]   {   smallest = r;   }     if (smallest != key)   {   Swap(ref heapArray[key],   ref heapArray[smallest]);   MinHeapify(smallest);   }  }    // Increases value of given key to new_val.  // It is assumed that new_val is greater  // than heapArray[key].  // Heapify from the given key  public void increaseKey(int key, int new_val)  {   heapArray[key] = new_val;   MinHeapify(key);  }    // Changes value on a key  public void changeValueOnAKey(int key, int new_val)  {   if (heapArray[key] == new_val)   {   return;   }   if (heapArray[key]   {   increaseKey(key, new_val);   } else  {   decreaseKey(key, new_val);   }  }  }    static class MinHeapTest{    // Driver code  public static void Main(string[] args)  {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);     Console.Write(h.extractMin() + ' ');   Console.Write(h.getMin() + ' ');     h.decreaseKey(2, 1);   Console.Write(h.getMin());  }  }    // This code is contributed by  // Dinesh Clinton Albert(dineshclinton)>

k Nächster-Nachbarn-Algorithmus

Javascript

// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest !== i)   {   [arr[i], arr[smallest]] = [arr[smallest], arr[i]]   this.MinHeapify(smallest);   }   }  }    let h = new MinHeap();   h.insert(3);   h.insert(2);   h.deleteKey(1);   h.insert(15);   h.insert(5);   h.insert(4);   h.insert(45);     console.log(h.extractMin() + ' ');   console.log(h.getMin() + ' ');     h.decreaseKey(2, 1);   console.log(h.extractMin());>

Ausgabe

2 4 1>

Anwendungen von Heaps:

Heap-Sortierung : Heap Sort verwendet Binary Heap, um ein Array in O(nLogn)-Zeit zu sortieren.
Prioritätswarteschlange: Prioritätswarteschlangen können mithilfe von Binary Heap effizient implementiert werden, da es die Operationen insert(), delete() und extractmax() sowie dependenceKey() in O(log N)-Zeit unterstützt. Binomial Heap und Fibonacci Heap sind Variationen von Binary Heap. Diese Variationen führen die Vereinigung auch effizient durch.
Graphalgorithmen: Die Prioritätswarteschlangen werden insbesondere in Graphalgorithmen wie verwendet Dijkstras kürzester Weg Und Prims Minimum Spanning Tree .
Viele Probleme können mit Heaps effizient gelöst werden. Siehe folgendes Beispiel. A) K'tes größtes Element in einem Array . B) Ein fast sortiertes Array sortieren/ C) K sortierte Arrays zusammenführen .

Verwandte Links:

Codierungspraxis auf Heap
Alle Artikel auf Heap
PriorityQueue: Binäre Heap-Implementierung in der Java-Bibliothek