A Gerichteter azyklischer Graph , oft abgekürzt als TAG ist ein grundlegendes Konzept der Graphentheorie. DAGs werden verwendet, um klar und geordnet darzustellen, wie Dinge zusammenhängen oder voneinander abhängen. In diesem Artikel werden wir mehr darüber erfahren Gerichteter azyklischer Graph , seine Eigenschaften und seine Anwendung im wirklichen Leben.

Gerichteter azyklischer Graph

Was ist ein gerichteter azyklischer Graph?

A Gerichteter azyklischer Graph (DAG) ist ein gerichteter Graph, der keine Zyklen enthält.

Das folgende Diagramm stellt einen gerichteten azyklischen Graphen (DAG) dar:

Direkter azyklischer Graph

Bedeutung des gerichteten azyklischen Graphen:

Der gerichtete azyklische Graph weist zwei wichtige Merkmale auf:

• Gerichtete Kante S:Im gerichteten azyklischen Graphen Jede Kante hat eine Richtung, das heißt, sie verläuft von einem Scheitelpunkt (Knoten) zum anderen. Diese Richtung bedeutet a Ein Weg Beziehung oder Abhängigkeit zwischen Knoten.
• Azyklisch: Der Begriff azyklisch zeigt an, dass es im Diagramm keine Zyklen oder geschlossenen Schleifen gibt. Mit anderen Worten: Sie können eine Folge gerichteter Kanten nicht durchlaufen und zum selben Knoten zurückkehren, indem Sie den Kantenrichtungen folgen. Die Bildung von Zyklen ist in verboten TAG. Daher ist diese Eigenschaft wesentlich.

Gerichteter azyklischer Graph

Eigenschaften des gerichteten azyklischen Graphen DAG:

Der gerichtete azyklische Graph (DAG) verfügt über verschiedene Eigenschaften, die ihn bei Diagrammproblemen einsetzbar machen.

Es gibt folgende Eigenschaften des gerichteten azyklischen Graphen (DAG):

• Erreichbarkeitsbeziehung: In DAG können wir feststellen, ob zwischen zwei Knoten eine Erreichbarkeitsbeziehung besteht. Knoten A gilt als von Knoten B aus erreichbar, wenn es einen gerichteten Pfad gibt, der bei Knoten B beginnt und bei Knoten A endet. Dies bedeutet, dass Sie der Richtung der Kanten im Diagramm folgen können, um von B nach A zu gelangen.
• Transitive Schließung: Der transitive Abschluss eines gerichteten Graphen ist ein neuer Graph, der alle direkten und indirekten Beziehungen oder Verbindungen zwischen Knoten im ursprünglichen Graphen darstellt. Mit anderen Worten: Es sagt Ihnen, welche Knoten von anderen Knoten aus erreicht werden können, indem Sie einer oder mehreren gerichteten Kanten folgen.

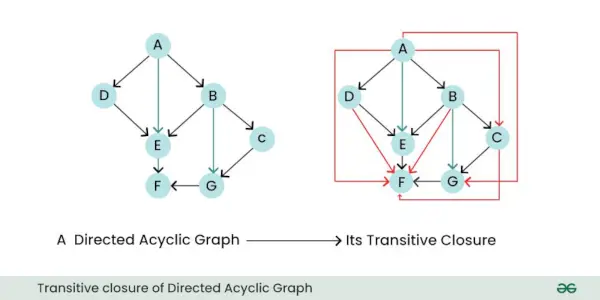
Transitiver Abschluss des gerichteten azyklischen Graphen

• Transitive Reduktion: Die transitive Reduktion eines gerichteten Graphen ist ein neuer Graph, der nur die wesentlichen direkten Beziehungen zwischen Knoten beibehält und gleichzeitig alle unnötigen indirekten Kanten entfernt. Im Wesentlichen vereinfacht es das Diagramm, indem es Kanten eliminiert, die aus den verbleibenden Kanten abgeleitet werden können.

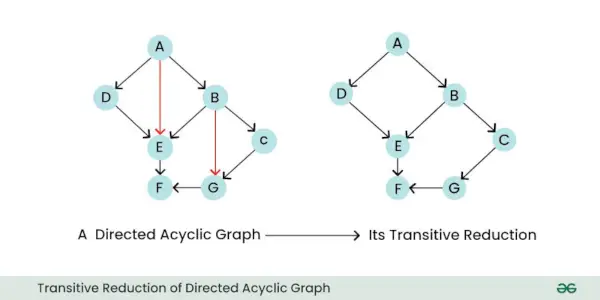
Transitive Reduktion des gerichteten azyklischen Graphen

• Topologische Reihenfolge: Eine DAG kann topologisch sortiert werden, was bedeutet, dass Sie ihre Knoten linear so anordnen können, dass bei allen Kanten der Startknoten der Kante früher in der Sequenz auftritt. Diese Eigenschaft ist für Aufgaben wie Planung und Abhängigkeitsauflösung nützlich.

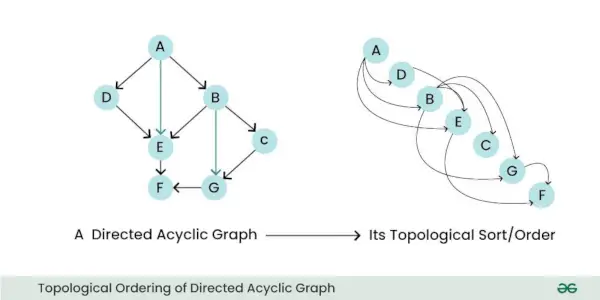
Topologische Ordnung des gerichteten azyklischen Graphen

Praktische Anwendungen von DAG:

• Datenflussanalyse: Beim Compiler-Design und bei der Compiler-Optimierung werden DAGs verwendet, um den Datenfluss innerhalb eines Programms darzustellen. Dies hilft bei der Codeoptimierung, indem redundante Berechnungen und toter Code identifiziert werden. DAGs werden auch verwendet, um die Struktur von darzustellen Grundblöcke im Compiler-Design.

• Aufgabenplanung: DAGs werden im Projektmanagement und bei der Jobplanung verwendet. Jede Aufgabe oder jeder Auftrag wird im DAG als Knoten dargestellt, wobei gerichtete Kanten Abhängigkeiten anzeigen. Die azyklische Natur des DAG stellt sicher, dass Aufgaben in einer logischen Reihenfolge geplant werden, wodurch zirkuläre Abhängigkeiten vermieden werden.

Zur Darstellung eines Planungsproblems kann ein gewichteter gerichteter azyklischer Graph verwendet werden. Nehmen wir das Beispiel eines Aufgabenplanungsproblems. Hier kann ein Scheitelpunkt die Aufgabe darstellen und sein Gewicht kann den Umfang der Aufgabenberechnung darstellen. Ebenso kann eine Kante die Kommunikation zwischen zwei Aufgaben darstellen und ihr Gewicht kann die Kommunikationskosten darstellen:

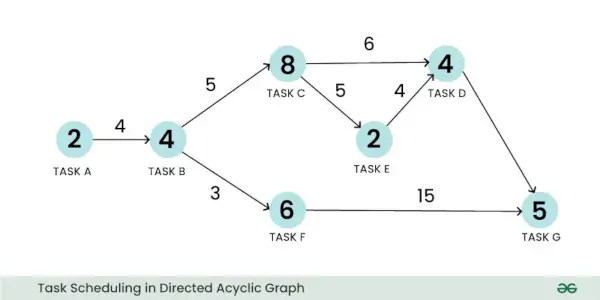
Aufgabenplanung im gerichteten azyklischen Graphen

Abschluss:

Zusammenfassend lässt sich sagen, dass gerichtete azyklische Graphen ein grundlegendes Konzept der Graphentheorie mit zahlreichen praktischen Anwendungen sind. DAGs spielen eine entscheidende Rolle bei der Aufgabenplanung, Datenflussanalyse, Abhängigkeitsauflösung und verschiedenen anderen Bereichen der Informatik und Technik. Sie helfen dabei, Prozesse zu optimieren, Abhängigkeiten zu verwalten und eine effiziente Ausführung von Aufgaben oder Jobs sicherzustellen.