Der Winkel zwischen zwei Vektoren ist der Winkel zwischen ihren Enden und dieser Winkel kann leicht mithilfe von Kreuzprodukt und Skalarprodukt von Vektorformeln ermittelt werden. Der Winkel zwischen zwei Vektoren liegt immer zwischen 0° und 180°.

In diesem Artikel erfahren Sie mehr über den Winkel zwischen zwei Vektoren, Definitionen, Formeln und Beispiele im Detail.

Was ist der Winkel zwischen zwei Vektoren?

Der Winkel zwischen zwei Vektoren ist der Winkel, der am Schnittpunkt ihrer Enden entsteht. Der Winkel zwischen zwei Vektoren kann je nach Richtung der Vektoren spitz, rechts oder stumpf sein.

Der Winkel zwischen zwei Vektoren wird mit zwei Formeln ermittelt:

• Verwenden des Skalarprodukts von Vektoren
• Verwendung des Kreuzprodukts von Vektoren

Dies wird in der folgenden Formel erläutert.

Winkel zwischen zwei Vektorformeln

Winkel zwischen zwei Vektoren lässt sich am einfachsten und am häufigsten mithilfe des Skalarprodukts von Vektoren finden.

Zwei Vektoren A und B

Skalarprodukt von A und B ist gegeben durch:

vec{A}.vec{B} = |A| |B| cosθ.

Sonderfälle

• Wenn der Winkel zwischen Vektoren 0 Grad beträgt.

Das ist θ = 0°

⇒ |A| |B| cosθ

⇒ |A| |B| cos0°

Gitterstruktur

⇒ |A| |B| [cos0° = 1]

• Wenn der Winkel zwischen Vektoren 180 Grad beträgt.

⇒ |A| |B| cosθ

⇒ |A| |B| cos180°

⇒ – |A| |B| [cos180° = -1]

• Wenn der Winkel zwischen Vektoren 90 Grad beträgt.

⇒ |A| |B| cosθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

Formel für den Winkel zwischen zwei Vektoren

Der Kosinus des Winkels zwischen zwei Vektoren ist gleich der Summe des Produkts der einzelnen Bestandteile der beiden Vektoren geteilt durch das Produkt der Größe der beiden Vektoren.

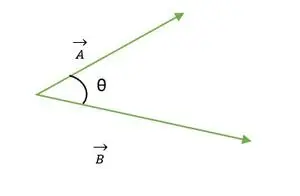
Zwei Vektoren A und B

vec{A}.vec{B} =| A | | B | cosθ.

cosθ=frac{vec{A}.vec{B}}B

θ= cos^-1 frac{vec{A}.vec{B}}B

In kartesischer Form,

A = A_Xich + A_Undj + A_Mitk

B= B_Xich + B_Undj + B_Mitk

cos θ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Eigenschaften des Dot-Produkts

• Skalarprodukt ist kommutativ

vec{A}.vec{B}=vec{B}.vec{A}

• Das Skalarprodukt ist distributiv

vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})

Der Winkel zwischen zwei Vektoren liegt zwischen 0 ≤ θ ≤ 180. Wenn die Enden oder Köpfe beider Vektoren zusammenfallen, wird der Winkel zwischen den Vektoren berechnet.

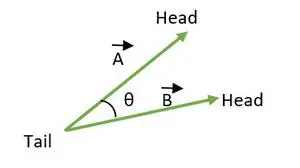
Schwanz zusammenfallen

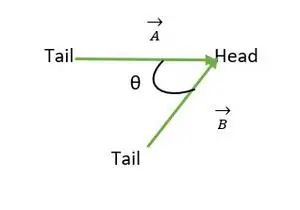
Kopfübereinstimmung

Beispielprobleme: Formel für den Winkel zwischen zwei Vektoren

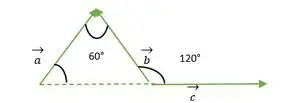
Aufgabe 1: Finden Sie den Winkel zwischen Vektoren (wenn sie ein gleichseitiges Dreieck bilden)

Array-Liste sortieren

• a- und b-Vektoren
• b- und c-Vektoren
• a- und c-Vektoren

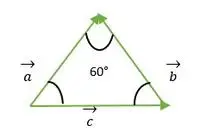
Gleichseitiges Dreieck, gebildet durch den Vektor a, b, c

Lösung:

• a- und b-Vektoren

Für die Vektoren a und b fallen die Spitzen beider Vektoren zusammen, daher ist der Winkel zwischen den Vektoren a und b derselbe wie der Winkel zwischen zwei Seiten eines gleichseitigen Dreiecks = 60°.

• b- und c-Vektoren:

Aus der obigen Abbildung sehen wir, dass Kopf oder Ende des b- und c-Vektors nicht miteinander übereinstimmen.

Durch die Verwendung der Eigenschaft bleibt ein Vektor unverändert, wenn er parallel zu sich selbst übertragen wird.

Der Vektor c wird parallel zu sich selbst verschoben

Jetzt sehen wir, dass die Enden der Vektoren b und c miteinander übereinstimmen und daher mit dem Außenwinkel eines gleichseitigen Dreiecks = 120° übereinstimmen.

• a- und c-Vektoren

Die Enden von a und c fallen zusammen

Bei den Vektoren a und c fallen die Enden beider Vektoren zusammen, daher ist der Winkel zwischen den Vektoren a und c derselbe wie der Winkel zwischen zwei Seiten des gleichseitigen Dreiecks = 60°.

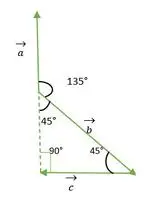
Aufgabe 2: Finden Sie Winkel zwischen Vektoren, wenn sie ein gleichschenkliges rechtwinkliges Dreieck bilden.

• a- und b-Vektor
• b- und c-Vektor
• a- und c-Vektoren

Lösung:

• a- und b-Vektor

Rechtwinkliges gleichschenkliges Dreieck

Aus der obigen Abbildung sehen wir, dass der Kopf oder Schwanz des a- und b-Vektors nicht miteinander übereinstimmt. Durch die Verwendung der Eigenschaft bleibt ein Vektor unverändert, wenn er parallel zu sich selbst übertragen wird.

ein Vektor wird parallel zu sich selbst verschoben

Nun fallen die Enden der Vektoren a und b zusammen und bilden einen Winkel, der dem Außenwinkel eines rechtwinkligen gleichschenkligen Dreiecks = 135° entspricht.

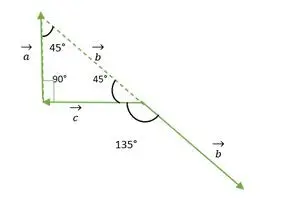
• b- und c-Vektor

Rechtwinkliges gleichschenkliges Dreieck

Aus der obigen Abbildung geht hervor, dass der Kopf oder Schwanz des b- und c-Vektors nicht miteinander übereinstimmt. Durch die Verwendung der Eigenschaft bleibt ein Vektor also unverändert, wenn er parallel zu sich selbst übertragen wird.

Der b-Vektor wird parallel zu sich selbst verschoben

Nun fallen die Enden der b- und c-Vektoren zusammen und bilden einen Winkel, der dem Außenwinkel eines rechtwinkligen gleichschenkligen Dreiecks = 135° entspricht.

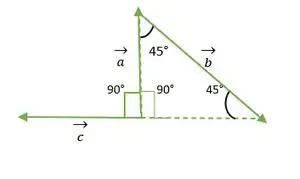
• a- und c-Vektoren

Rechtwinkliges gleichschenkliges Dreieck

Aus der obigen Abbildung geht hervor, dass der Kopf bzw. die Enden der Vektoren a und c nicht miteinander übereinstimmen. Durch die Verwendung der Eigenschaft bleibt ein Vektor unverändert, wenn er parallel zu sich selbst übertragen wird.

Der c-Vektor wird parallel zu sich selbst verschoben

Nun fallen die Enden der Vektoren a und c zusammen und bilden einen Winkel, der dem rechten Winkel eines gleichschenkligen Dreiecks = 90° entspricht.

Aufgabe 3: Finden Sie den Winkel zwischen den Vektoren A = i + j + k und dem Vektor B = -2i – 2j – 2k.

Lösung:

Aus der Formel,

mylivecriclet

A = A_Xich + A_Undj + A_Mitk

B= B_Xich + B_Undj + B_Mitk

cosθ=frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Hier in der gegebenen Frage:

A= i + j + k

B= -2i -2j -2k

Ersetzen der Werte in der Formel

⇒ cosθ =frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})}

⇒ cosθ =frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})}

⇒ cosθ =frac{-6}{(sqrt{3}×sqrt{12})}

⇒ cosθ =frac{-6}{(sqrt{36})}

⇒ cosθ = -6/6

⇒ cosθ= -1

⇒ θ = 180°

Aufgabe 4: Finden Sie den Winkel zwischen Vektor A = 3i + 4j und B = 2i + j

Python // Operator

Lösung:

A = A_Xich + A_Undj + A_Mitk

B = B_Xich + B_Undj + B_Mitk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Hier gegeben,

A= 3i + 4j + 0k

B= 2i + j + 0k

Ersetzen der Werte in der Formel,

⇒ cosθ =frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})}

⇒ cosθ =frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})}

⇒ cosθ =frac{(10)}{(sqrt{25}×sqrt{5})}

⇒ cosθ =frac{(10)}{(sqrt{125})}

⇒ θ = cos^-1(frac{(10)}{5.(sqrt{5})})

⇒ θ = cos^-1(frac{2}{(sqrt{5})})

Aufgabe 5: Finden Sie den Winkel zwischen Vektor A = i + j und Vektor B = j + k.

Wie groß ist mein Monitor?

Lösung:

Aus der Formel,

A = A_Xich + A_Undj + A_Mitk

B = B_Xich + B_Undj + B_Mitk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Hier in der gegebenen Frage:

⇒ A = i + j

⇒ B = j + k

⇒ cosθ =frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})}

⇒ cosθ =frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})}

⇒ cosθ =frac{1}{(sqrt{2}×sqrt{2})}

⇒ θ = cos^-1(1/2)

⇒ θ = 60°