EINFÜHRUNG IN MIN-HEAP – DATENSTRUKTUR- UND ALGORITHMUS-TUTORIALS

A Min-Heap ist als eine Art von definiert Die Heap-Datenstruktur ist eine Art Binärbaum, der in der Informatik häufig für verschiedene Zwecke verwendet wird, einschließlich Sortieren, Suchen und Organisieren von Daten.

Einführung in Min-Heap – Tutorials zu Datenstruktur und Algorithmen

Zweck und Anwendungsfälle von Min-Heap:

Prioritätswarteschlange implementieren: Eine der Hauptverwendungen der Heap-Datenstruktur ist die Implementierung von Prioritätswarteschlangen.
Dijkstras Algorithmus : Der Dijkstra-Algorithmus ist ein Kürzeste-Pfad-Algorithmus, der den kürzesten Pfad zwischen zwei Knoten in einem Diagramm findet. Ein Min-Heap kann verwendet werden, um die nicht besuchten Knoten mit der geringsten Entfernung vom Quellknoten zu verfolgen.
Sortierung: Ein Min-Heap kann als Sortieralgorithmus verwendet werden, um eine Sammlung von Elementen effizient in aufsteigender Reihenfolge zu sortieren.
Medianer Befund: Ein Min-Heap kann verwendet werden, um den Median eines Zahlenstroms effizient zu ermitteln. Wir können einen Min-Heap verwenden, um die größere Hälfte der Zahlen zu speichern, und einen Max-Heap, um die kleinere Hälfte zu speichern. Der Median ist die Wurzel des Min-Heaps.

Min-Heap-Datenstruktur in verschiedenen Sprachen:

1. Min-Heap in C++

Ein Min-Heap kann mit implementiert werden Prioritätswarteschlange Container aus der Standard Template Library (STL). Der Prioritätswarteschlange Container ist eine Art Containeradapter, der eine Möglichkeit bietet, Elemente in einer warteschlangenähnlichen Datenstruktur zu speichern, in der jedem Element eine Priorität zugeordnet ist.

Syntax :

C++

 priority_queue < int, vector , größer > minH;>

2. Min-Heap in Java

In Java kann ein Min-Heap mit implementiert werden Prioritätswarteschlange Klasse von java.util-Paket . Die PriorityQueue-Klasse ist eine Prioritätswarteschlange, die eine Möglichkeit bietet, Elemente in einer warteschlangenähnlichen Datenstruktur zu speichern, in der jedem Element eine Priorität zugeordnet ist.

Java-equals-Methode

Syntax :

Java

 PriorityQueue minHeap = neue PriorityQueue ();>

3. Min-Heap in Python

In Python kann ein Min-Heap mit implementiert werden Heapq Modul, das Funktionen zur Implementierung von Heaps bereitstellt. Konkret die Heapq Das Modul bietet eine Möglichkeit, Heap-Datenstrukturen zu erstellen und zu bearbeiten.

Syntax:

Python

 heap = [] heapify(heap)>

4. Min-Heap in C#

In C# kann ein Min-Heap mithilfe der PriorityQueue-Klasse aus dem implementiert werden System.Collections.Generic-Namespace . Die PriorityQueue-Klasse ist eine Prioritätswarteschlange, die eine Möglichkeit bietet, Elemente in einer warteschlangenähnlichen Datenstruktur zu speichern, in der jedem Element eine Priorität zugeordnet ist.

Syntax:

 var minHeap = new PriorityQueue ();>

5. Min-Heap in JavaScript

Ein Min-Heap ist ein Binärbaum, in dem jeder Knoten einen Wert hat, der kleiner oder gleich dem Wert seiner untergeordneten Knoten ist. In JavaScript können Sie einen minimalen Heap mithilfe eines Arrays implementieren, wobei das erste Element den Wurzelknoten und die untergeordneten Elemente eines Knotens den Index darstellen ich befinden sich an Indizes 2i+1 Und 2i+2.

Syntax:

JavaScript

 const minHeap = new MinHeap();>

Unterschied zwischen Min Heap und Max Heap:

	Min. Heap	Max Heap
1.	In einem Min-Heap muss der am Wurzelknoten vorhandene Schlüssel kleiner oder gleich den Schlüsseln aller seiner untergeordneten Knoten sein.	In einem Max-Heap muss der am Wurzelknoten vorhandene Schlüssel größer oder gleich den Schlüsseln aller seiner untergeordneten Knoten sein.
2.	In einem Min-Heap ist das minimale Schlüsselelement an der Wurzel vorhanden.	In einem Max-Heap ist das maximale Schlüsselelement im Root vorhanden.
3.	Ein Min-Heap verwendet die aufsteigende Priorität.	Ein Max-Heap verwendet die absteigende Priorität.
4.	Beim Aufbau eines Min-Heaps hat das kleinste Element Vorrang.	Beim Aufbau eines Max-Heaps hat das größte Element Vorrang.
5.	In einem Min-Heap wird das kleinste Element als erstes aus dem Heap entfernt.	In einem Max-Heap wird das größte Element als erstes aus dem Heap entfernt.

Interne Implementierung der Min-Heap-Datenstruktur:

A Min. Heap wird normalerweise als Array dargestellt .

Das Stammelement befindet sich unter Arr[0] .
Für jeden i-ten Knoten Arr[i] :
Arr[(i -1) / 2] gibt seinen übergeordneten Knoten zurück.
Arr[(2 * i) + 1] gibt seinen linken untergeordneten Knoten zurück.
Arr[(2 * i) + 2] gibt seinen rechten untergeordneten Knoten zurück.

Die interne Implementierung des Min-Heap erfordert drei Hauptschritte:

Einfügen : Um ein Element in den Min-Heap einzufügen, hängen wir das Element zunächst an das Ende des Arrays an und passen dann die Heap-Eigenschaft an, indem wir das Element wiederholt mit seinem übergeordneten Element austauschen, bis es sich an der richtigen Position befindet.
Streichung : Um das minimale Element aus dem Min-Heap zu entfernen, tauschen wir zuerst den Wurzelknoten mit dem letzten Element im Array aus, entfernen das letzte Element und passen dann die Heap-Eigenschaft an, indem wir das Element wiederholt mit seinem kleinsten untergeordneten Element austauschen, bis es im Array ist Korrekte Position.
Aufhäufen : Eine Heapify-Operation kann verwendet werden, um einen Min-Heap aus einem unsortierten Array zu erstellen.

Operationen an der Min-Heap-Datenstruktur und ihre Implementierung:

Hier sind einige allgemeine Vorgänge, die für eine Heap-Datenstruktur ausgeführt werden können:

1. Einfügen in die Min-Heap-Datenstruktur :

Elemente können nach einem ähnlichen Ansatz wie oben zum Löschen beschrieben in den Heap eingefügt werden. Die Idee ist:

Der Einfügevorgang in einem Min-Heap umfasst die folgenden Schritte:
Fügen Sie das neue Element am Ende des Heaps an der nächsten verfügbaren Position in der letzten Ebene des Baums hinzu.
Vergleichen Sie das neue Element mit seinem übergeordneten Element. Wenn das übergeordnete Element größer als das neue Element ist, tauschen Sie es aus.
Wiederholen Sie Schritt 2, bis das übergeordnete Element kleiner oder gleich dem neuen Element ist oder bis das neue Element die Wurzel des Baums erreicht.
Das neue Element befindet sich nun an der richtigen Position im Min-Heap und die Heap-Eigenschaft ist erfüllt.

Illustration:

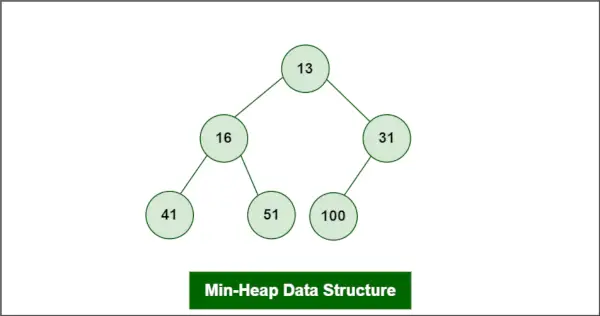
Angenommen, der Heap ist ein Min-Heap wie folgt:

Einfügen in Min-Heap

Implementierung der Einfügungsoperation in Min-Heap:

C++

 #include  #include  using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Füge das neue Element am Ende des Heaps hinzu heap.push_back(value);  // Den Index des letzten Elements abrufen int index = heap.size() - 1;  // Das neue Element mit seinem übergeordneten Element vergleichen und bei Bedarf // austauschen while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]);  // Im Baum nach oben zum übergeordneten Element des aktuellen // Elements verschieben index = (index - 1) / 2;  } } // Hauptfunktion zum Testen der Funktion insert_min_heap int main() { vector Haufen;  int-Werte[] = { 10, 7, 11, 5, 4, 13 };  int n = sizeof(values) / sizeof(values[0]);  für (int i = 0; i< n; i++) {  insert_min_heap(heap, values[i]);  cout << 'Inserted ' << values[i]  << ' into the min-heap: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  }  return 0; }>

Java

 import java.util.*; public class GFG {  // Function to insert a new element into the min-heap  public static void insertMinHeap(int[] heap, int size,  int value)  {  // Add the new element to the end of the heap  heap[size] = value;  // Get the index of the last element  int index = size;  // Compare the new element with its parent and swap  // if necessary  while (index>0 && heap[(index - 1) / 2]> heap[index]) { swap(heap, index, (index - 1) / 2);  // Im Baum nach oben zum übergeordneten Element des aktuellen // Elements verschieben index = (index - 1) / 2;  } } // Funktion zum Austauschen zweier Elemente in einem Array public static void swap(int[] arr, int i, int j) { int temp = arr[i];  arr[i] = arr[j];  arr[j] = temp;  } // Hauptfunktion zum Testen der insertMinHeap-Funktion public static void main(String[] args) { int[] heap = new int[6];  int[] Werte = { 10, 7, 11, 5, 4, 13 };  int-Größe = 0;  für (int i = 0; i< values.length; i++) {  insertMinHeap(heap, size, values[i]);  size++;  System.out.print('Inserted ' + values[i]  + ' into the min-heap: ');  for (int j = 0; j < size; j++) {  System.out.print(heap[j] + ' ');  }  System.out.println();  }  } }>

Python3

 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 und heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ index] # Im Baum nach oben zum übergeordneten Element des aktuellen Elements verschieben index = (index - 1) // 2 heap = [] Werte = [10, 7, 11, 5, 4, 13] für Wert in Werte: insert_min_heap( Heap, Wert) print(f'{Wert} in den Min-Heap eingefügt: {heap}')>

 using System; using System.Collections.Generic; public class Program {  // Function to insert a new element into the min-heap  static void InsertMinHeap(List heap, int value) { // Füge das neue Element am Ende des Heaps hinzu heap.Add(value);  // Den Index des letzten Elements abrufen int index = heap.Count - 1;  // Das neue Element mit seinem übergeordneten Element vergleichen und ggf. austauschen // while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index];  heap[index] = heap[(index - 1) / 2];  heap[(index - 1) / 2] = temp;  // Im Baum nach oben zum übergeordneten Element des aktuellen // Elements verschieben index = (index - 1) / 2;  } } // Hauptfunktion zum Testen der InsertMinHeap-Funktion public static void Main() { List Heap = neue Liste ();  int[] Werte = { 10, 7, 11, 5, 4, 13 };  foreach(int-Wert in Werten) { InsertMinHeap(heap, value);  Console.Write('Inserted ' + value + ' into the min-heap: ');  foreach(int element in heap) { Console.Write(element + ' ');  } Console.WriteLine();  } } }>

Javascript

 function insertMinHeap(heap, value) {  heap.push(value);  let index = heap.length - 1;  let parentIndex = Math.floor((index - 1) / 2);  while (index>0 && heap[parentIndex]> heap[index]) { [heap[index], heap[parentIndex]] = [heap[parentIndex], heap[index]];  index = parentIndex;  parentIndex = Math.floor((index - 1) / 2);  } } // Beispielverwendung const heap = []; const-Werte = [10, 7, 11, 5, 4, 13]; for (konstanter Wert der Werte) { insertMinHeap(heap, value);  console.log(`${value} in den Min-Heap eingefügt: ${heap}`); }>

Ausgabe

Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>

Zeitkomplexität: O(log(n)) ( wobei n die Anzahl der Elemente im Heap ist )
Hilfsraum: An)

2. Löschen in der Min-Heap-Datenstruktur :

Entfernen des kleinsten Elements (der Wurzel) aus dem Min-Heap. Die Wurzel wird durch das letzte Element im Heap ersetzt, und dann wird die Heap-Eigenschaft wiederhergestellt, indem die neue Wurzel mit ihrem kleinsten untergeordneten Element ausgetauscht wird, bis das übergeordnete Element kleiner als beide untergeordneten Elemente ist oder bis die neue Wurzel einen Blattknoten erreicht.

Ersetzen Sie den Stamm oder das zu löschende Element durch das letzte Element.
Löschen Sie das letzte Element aus dem Heap.
Da das letzte Element nun an der Position des Wurzelknotens platziert ist. Daher folgt es möglicherweise nicht der Heap-Eigenschaft. Heapifizieren Sie daher den letzten Knoten, der an der Position der Wurzel platziert ist.

Illustration :

Angenommen, der Heap ist ein Min-Heap wie folgt:
Endlosschleife

Min-Heap-Datenstruktur

Das zu löschende Element ist root, also 13.

Verfahren :

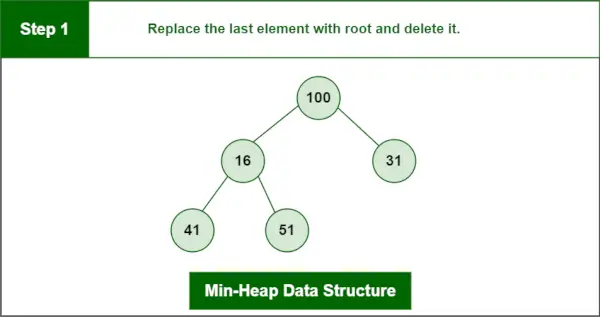
Das letzte Element ist 100.

Schritt 1: Ersetzen Sie das letzte Element durch root und löschen Sie es.

Min-Heap-Datenstruktur

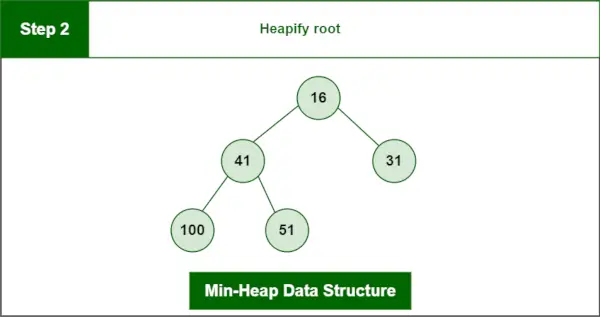
Schritt 2 : Wurzel aufhäufen.

Letzter Haufen:

Min-Heap-Datenstruktur

Implementierung des Löschvorgangs in Min-Heap:

C++

 #include  #include  using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Füge das neue Element am Ende des Heaps hinzu heap.push_back(value);  // Den Index des letzten Elements abrufen int index = heap.size() - 1;  // Das neue Element mit seinem übergeordneten Element vergleichen und bei Bedarf // austauschen while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]);  // Im Baum nach oben zum übergeordneten Element des aktuellen // Elements verschieben index = (index - 1) / 2;  } } // Funktion zum Löschen eines Knotens aus dem Min-Heap void delete_min_heap(vector & heap, int value) { // Finden Sie den Index des zu löschenden Elements int index = -1;  für (int i = 0; i< heap.size(); i++) {  if (heap[i] == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last  // element  heap[index] = heap[heap.size() - 1];  // Remove the last element  heap.pop_back();  // Heapify the tree starting from the element at the  // deleted index  while (true) {  int left_child = 2 * index + 1;  int right_child = 2 * index + 2;  int smallest = index;  if (left_child < heap.size()  && heap[left_child] < heap[smallest]) {  smallest = left_child;  }  if (right_child < heap.size()  && heap[right_child] < heap[smallest]) {  smallest = right_child;  }  if (smallest != index) {  swap(heap[index], heap[smallest]);  index = smallest;  }  else {  break;  }  } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() {  vector Haufen;  int-Werte[] = { 13, 16, 31, 41, 51, 100 };  int n = sizeof(values) / sizeof(values[0]);  für (int i = 0; i< n; i++) {  insert_min_heap(heap, values[i]);  }  cout << 'Initial heap: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  delete_min_heap(heap, 13);  cout << 'Heap after deleting 13: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  return 0; }>

Java

 import java.util.*; public class GFG {  // Function to insert a new element into the min-heap  public static void insertMinHeap(List heap, int value) { // Das neue Element am Ende des Heaps hinzufügen heap.add(value);  // Den Index des letzten Elements abrufen int index = heap.size() - 1;  // Das neue Element mit seinem übergeordneten Element vergleichen und ggf. austauschen // while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (Index - 1) / 2);  // Im Baum nach oben zum übergeordneten Element des aktuellen // Elements verschieben index = (index - 1) / 2;  } } // Funktion zum Löschen eines Knotens aus dem Min-Heap public static void deleteMinHeap(List heap, int value) { // Finden Sie den Index des zu löschenden Elements int index = -1;  für (int i = 0; i< heap.size(); i++) {  if (heap.get(i) == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last  // element  heap.set(index, heap.get(heap.size() - 1));  // Remove the last element  heap.remove(heap.size() - 1);  // Heapify the tree starting from the element at the  // deleted index  while (true) {  int leftChild = 2 * index + 1;  int rightChild = 2 * index + 2;  int smallest = index;  if (leftChild < heap.size()  && heap.get(leftChild)  < heap.get(smallest)) {  smallest = leftChild;  }  if (rightChild < heap.size()  && heap.get(rightChild)  < heap.get(smallest)) {  smallest = rightChild;  }  if (smallest != index) {  Collections.swap(heap, index, smallest);  index = smallest;  }  else {  break;  }  }  }  // Main function to test the insertMinHeap and  // deleteMinHeap functions  public static void main(String[] args)  {  List heap = neue ArrayList ();  int[] Werte = { 13, 16, 31, 41, 51, 100 };  int n = Werte.Länge;  für (int i = 0; i< n; i++) {  insertMinHeap(heap, values[i]);  }  System.out.print('Initial heap: ');  for (int j = 0; j < heap.size(); j++) {  System.out.print(heap.get(j) + ' ');  }  System.out.println();  deleteMinHeap(heap, 13);  System.out.print('Heap after deleting 13: ');  for (int j = 0; j < heap.size(); j++) {  System.out.print(heap.get(j) + ' ');  }  System.out.println();  } }>

Python3

 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 und heap[(index - 1) // 2]> heap[index]: heap[index], heap[(index - 1) // 2] = heap[(index - 1) // 2], heap[ index] index = (index - 1) // 2 def delete_min_heap(heap, value): index = -1 for i in range(len(heap)): if heap[i] == value: index = i break if index == -1: return heap[index] = heap[-1] heap.pop() while True: left_child = 2 * index + 1 right_child = 2 * index + 2 kleinster = Index, wenn left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)>

 using System; using System.Collections.Generic; class MinHeap {  private List Heap = neue Liste ();  public void Insert(int value) { heap.Add(value);  int index = heap.Count - 1;  while (index> 0 && heap[(index - 1) / 2]> heap[index]) { Swap(index, (index - 1) / 2);  Index = (Index - 1) / 2;  } } public void Delete(int value) { int index = heap.IndexOf(value);  if (index == -1) { return;  } heap[index] = heap[heap.Count - 1];  heap.RemoveAt(heap.Count - 1);  while (true) { int leftChild = 2 * index + 1;  int rightChild = 2 * index + 2;  int kleinster = index;  if (leftChild< heap.Count  && heap[leftChild] < heap[smallest]) {  smallest = leftChild;  }  if (rightChild < heap.Count  && heap[rightChild] < heap[smallest]) {  smallest = rightChild;  }  if (smallest != index) {  Swap(index, smallest);  index = smallest;  }  else {  break;  }  }  }  private void Swap(int i, int j)  {  int temp = heap[i];  heap[i] = heap[j];  heap[j] = temp;  }  public void Print()  {  for (int i = 0; i < heap.Count; i++) {  Console.Write(heap[i] + ' ');  }  Console.WriteLine();  } } class Program {  static void Main(string[] args)  {  MinHeap heap = new MinHeap();  int[] values = { 13, 16, 31, 41, 51, 100 };  for (int i = 0; i < values.Length; i++) {  heap.Insert(values[i]);  }  Console.Write('Initial heap: ');  heap.Print();  heap.Delete(13);  Console.Write('Heap after deleting 13: ');  heap.Print();  } }>

Javascript

 function insertMinHeap(heap, value) {  // Add the new element to the end of the heap  heap.push(value);  // Get the index of the last element  let index = heap.length - 1;  // Compare the new element with its parent and swap if necessary  for (let flr = Math.floor((index - 1) / 2); index>0 && heap[flr]> heap[index]; flr = Math.floor((index - 1) / 2)) { [heap[index], heap[flr]] = [ heap[flr], heap[index], ];  // Im Baum nach oben zum übergeordneten Element des aktuellen Elements verschieben index = Math.floor((index - 1) / 2);  } } function deleteMinHeap(heap, value) { // Index des zu löschenden Elements finden let index = -1;  für (sei i = 0; i< heap.length; i++) {  if (heap[i] == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last element  heap[index] = heap[heap.length - 1];  // Remove the last element  heap.pop();  // Heapify the tree starting from the element at the deleted index  while (true) {  let left_child = 2 * index + 1;  let right_child = 2 * index + 2;  let smallest = index;  if (left_child < heap.length && heap[left_child] < heap[smallest]) {  smallest = left_child;  }  if (right_child < heap.length && heap[right_child] < heap[smallest]) {  smallest = right_child;  }  if (smallest != index) {  [heap[index], heap[smallest]] = [heap[smallest], heap[index]];  index = smallest;  } else {  break;  }  } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) {  insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));>

Ausgabe

Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>

Zeitkomplexität : O(log n) wobei n die Anzahl der Elemente im Heap ist
Hilfsraum: An)

3. Peek-Operation für die Min-Heap-Datenstruktur:

Um auf das minimale Element (d. h. die Wurzel des Heaps) zuzugreifen, wird der Wert des Wurzelknotens zurückgegeben. Die zeitliche Komplexität von Peek in einem Min-Heap beträgt O(1).

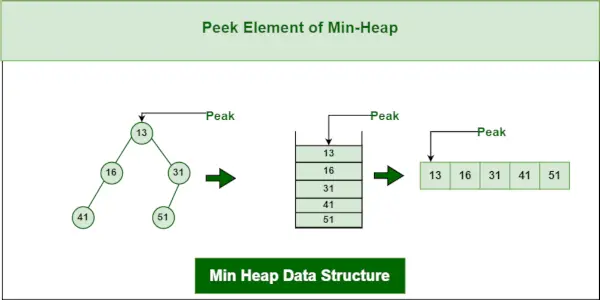
Min. Heap-Datenstruktur

Implementierung der Peek-Operation in Min-Heap:

C++

 #include  #include  #include  using namespace std; int main() {  // Create a max heap with some elements using a  // priority_queue  priority_queue , größer > minHeap;  minHeap.push(9);  minHeap.push(8);  minHeap.push(7);  minHeap.push(6);  minHeap.push(5);  minHeap.push(4);  minHeap.push(3);  minHeap.push(2);  minHeap.push(1);  // Holen Sie sich das Peak-Element (d. h. das größte Element) int PeakElement = minHeap.top();  // Den Peak-Element-Cout ausgeben<< 'Peak element: ' << peakElement << std::endl;  return 0; }>

Java

 import java.util.PriorityQueue; public class GFG {  public static void main(String[] args)  {  // Create a max heap with some elements using a  // PriorityQueue  PriorityQueue minHeap = new PriorityQueue();  minHeap.add(9);  minHeap.add(8);  minHeap.add(7);  minHeap.add(6);  minHeap.add(5);  minHeap.add(4);  minHeap.add(3);  minHeap.add(2);  minHeap.add(1);  // Holen Sie sich das Peak-Element (d. h. das größte Element) int PeakElement = minHeap.peek();  // Peak-Element drucken System.out.println('Peak element: ' +peakElement);  } }>

Python3

 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)>

 using System; using System.Collections.Generic; public class GFG {  public static void Main()  {  // Create a min heap with some elements using a  // PriorityQueue  var minHeap = new PriorityQueue ();  minHeap.Enqueue(9);  minHeap.Enqueue(8);  minHeap.Enqueue(7);  minHeap.Enqueue(6);  minHeap.Enqueue(5);  minHeap.Enqueue(4);  minHeap.Enqueue(3);  minHeap.Enqueue(2);  minHeap.Enqueue(1);  // Holen Sie sich das Peak-Element (d. h. das kleinste Element) int PeakElement = minHeap.Peek();  // Peak-Element ausgeben Console.WriteLine('Peak element: ' +peakElement);  } }>

Javascript

 const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Holen Sie sich das Peak-Element (d. h. das kleinste Element) const PeakElement = minHeap.peek(); // Das Peak-Element ausgeben console.log(`Peak element: ${peakElement}`);>

Ausgabe

Peak element: 1>

Zeitkomplexität : In einem Min-Heap, der mithilfe eines Arrays oder einer Liste implementiert wird, kann auf das Peak-Element in konstanter Zeit, O(1), zugegriffen werden, da es sich immer im Stammverzeichnis des Heaps befindet.
In einem mit einem Binärbaum implementierten Min-Heap kann auf das Peak-Element auch in O(1)-Zeit zugegriffen werden, da es sich immer an der Wurzel des Baums befindet.

Hilfsraum: An)

4. Heapify-Vorgang für die Min-Heap-Datenstruktur:

Mit einer Heapify-Operation kann aus einem unsortierten Array ein Min-Heap erstellt werden. Dazu wird am letzten Nicht-Blattknoten begonnen und der Bubble-Down-Vorgang wiederholt ausgeführt, bis alle Knoten die Heap-Eigenschaft erfüllen.

Gimp-Rechteck zeichnen

Heapify-Vorgang in Min Heap

Implementierung der Heapify-Operation in Min-Heap:

C++

 #include  #include  using namespace std; void minHeapify(vector &arr, int i, int n) { int kleinste = i;  int l = 2*i + 1;  int r = 2*i + 2;  wenn (l< n && arr[l] < arr[smallest])  smallest = l;  if (r < n && arr[r] < arr[smallest])  smallest = r;  if (smallest != i) {  swap(arr[i], arr[smallest]);  minHeapify(arr, smallest, n);  } } int main() {  vector arr = {10, 5, 15, 2, 20, 30};  cout<< 'Original array: ';  for (int i = 0; i < arr.size(); i++)  cout << arr[i] << ' ';  // Perform heapify operation on min-heap  for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size());  cout<< '
Min-Heap after heapify operation: ';  for (int i = 0; i < arr.size(); i++)  cout << arr[i] << ' ';  return 0; }>

Java

 // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main {  // Function to maintain the min-heap property of the heap rooted at index 'i'  public static void minHeapify(List arr, int i, int n) { // Angenommen, die Wurzel ist zunächst das kleinste Element int small = i;  // Berechnen Sie die Indizes des linken und rechten Kindes des aktuellen Knotens int l = 2 * i + 1;  int r = 2 * i + 2;  // Vergleiche das linke Kind mit dem aktuell kleinsten if (l< n && arr.get(l) < arr.get(smallest))  smallest = l;  // Compare the right child with the current smallest  if (r < n && arr.get(r) < arr.get(smallest))  smallest = r;  // If the current node is not the smallest, swap it with the smallest child  if (smallest != i) {  int temp = arr.get(i);  arr.set(i, arr.get(smallest));  arr.set(smallest, temp);  // Recursively heapify the subtree rooted at the smallest child  minHeapify(arr, smallest, n);  }  }  public static void main(String[] args) {  // Create a list representing the array  List arr = Arrays.asList(10, 5, 15, 2, 20, 30);  System.out.print('Original-Array: ');  // Original-Array drucken for (int i = 0; i< arr.size(); i++)  System.out.print(arr.get(i) + ' ');  // Perform heapify operation on the min-heap  // Start from the last non-leaf node and go up to the root of the tree  for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size());  System.out.print('
Min-Heap nach Heapify-Vorgang: ');  // Den Min-Heap nach dem Heapify-Vorgang drucken for (int i = 0; i< arr.size(); i++)  System.out.print(arr.get(i) + ' ');  } }>

Python

 def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)>

 using System; using System.Collections.Generic; class GFG {  // Function to perform the minHeapify operation on a min-heap.  static void MinHeapify(List arr, int i, int n) { int kleinste = i;  int left = 2 * i + 1;  int right = 2 * i + 2;  // Vergleiche den linken untergeordneten Knoten mit dem aktuell kleinsten Knoten.  wenn (links< n && arr[left] < arr[smallest])  smallest = left;  // Compare the right child with the current smallest node.  if (right < n && arr[right] < arr[smallest])  smallest = right;  // If the current node is not the smallest  // swap it with the smallest child.  if (smallest != i)  {  int temp = arr[i];  arr[i] = arr[smallest];  arr[smallest] = temp;  // Recursively call minHeapify on the affected subtree.  MinHeapify(arr, smallest, n);  }  }  static void Main(string[] args)  {  List arr = neue Liste { 10, 5, 15, 2, 20, 30 };  Console.Write('Original-Array: ');  foreach (int num in arr) Console.Write(num + ' ');  // Heapify-Vorgang für den Min-Heap ausführen.  for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count);  Console.Write('
Min-Heap nach Heapify-Vorgang: ');  foreach (int num in arr) Console.Write(num + ' ');  } }>

Javascript

 // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) {  let smallest = i;  let l = 2 * i + 1;  let r = 2 * i + 2;  // Check if left child is smaller than the current smallest element  if (l < n && arr[l] < arr[smallest])  smallest = l;  // Check if right child is smaller than the current smallest element  if (r < n && arr[r] < arr[smallest])  smallest = r;  // If the smallest element is not the current element, swap them  if (smallest !== i) {  [arr[i], arr[smallest]] = [arr[smallest], arr[i]];  minHeapify(arr, smallest, n);  } } // Main function function main() {  const arr = [10, 5, 15, 2, 20, 30];  // Print the original array  console.log('Original array: ' + arr.join(' '));  // Perform heapify operation on the min-heap  for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length);  // Den Min-Heap nach dem Heapify-Vorgang drucken console.log('Min-Heap nach dem Heapify-Vorgang: ' + arr.join(' ')); } // Rufen Sie die Hauptfunktion auf, um den Prozess zu starten main();>

Ausgabe

Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>

Die zeitliche Komplexität der Heapifizierung in einem Min-Heap beträgt O(n).

5. Suchvorgang für die Min-Heap-Datenstruktur:

Um nach einem Element im Min-Heap zu suchen, kann eine lineare Suche über das Array durchgeführt werden, das den Heap darstellt. Die zeitliche Komplexität einer linearen Suche beträgt jedoch O(n), was nicht effizient ist. Daher ist die Suche in einem Min-Heap kein häufig verwendeter Vorgang.

Hier ist ein Beispielcode, der zeigt, wie man mit nach einem Element in einem Min-Heap sucht std::find() :

C++

 #include  using namespace std; int main() {  priority_queue , größer > min_heap;  // Beispiel für maximalen Heap min_heap.push(10);  min_heap.push(9);  min_heap.push(8);  min_heap.push(6);  min_heap.push(4);  int element = 6; // Element zum Suchen nach bool found = false;  // Kopieren Sie den Min-Heap in eine temporäre Warteschlange und suchen Sie // nach dem Element std::priority_queue , größer > temp = min_heap;  while (!temp.empty()) { if (temp.top() == element) { Found = true;  brechen;  } temp.pop();  } if (found) { std::cout<< 'Element found in the min heap.'  << std::endl;  }  else {  std::cout << 'Element not found in the min heap.'  << std::endl;  }  return 0; }>

Java

 import java.util.PriorityQueue; public class GFG {  public static void main(String[] args)  {  PriorityQueue min_heap = new PriorityQueue();  min_heap.add( 3); // Elemente in die Prioritätswarteschlange einfügen min_heap.offer(1);  min_heap.offer(4);  min_heap.offer(1);  min_heap.offer(6);  int element = 6; // Element zum Suchen nach Boolean Found = false;  // Kopieren Sie den Min-Heap in eine temporäre Warteschlange und suchen Sie // nach dem Element PriorityQueue temp = new PriorityQueue(min_heap);  while (!temp.isEmpty()) { if (temp.poll() == element) { Found = true;  brechen;  } } if (found) { System.out.println( 'Element im Min-Heap gefunden.');  } else { System.out.println( 'Element nicht im Min-Heap gefunden.');  } } }>

Python3

 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')>

 using System; using System.Collections.Generic; public class GFG {  public static void Main()  {  var minHeap = new PriorityQueue ();  // Beispiel min Heap minHeap.Enqueue(4);  minHeap.Enqueue(6);  minHeap.Enqueue(8);  minHeap.Enqueue(9);  minHeap.Enqueue(10);  int element = 6; // Element zum Suchen nach bool found = false;  // Kopieren Sie den Min-Heap in eine temporäre Warteschlange und suchen Sie // nach dem Element var temp = new PriorityQueue (minHeap);  while (temp.Count> 0) { if (temp.Peek() == element) { Found = true;  brechen;  } temp.Dequeue();  } if (found) { Console.WriteLine( 'Element im Min-Heap gefunden.');  } else { Console.WriteLine( 'Element nicht im Min-Heap gefunden.');  } } }>

Javascript

 // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == element) { Found = true;  brechen;  } temp.dequeue(); } if (found) { console.log('Element im Min-Heap gefunden.'); } else { console.log('Element nicht im Min-Heap gefunden.'); }>

Ausgabe

Element found in the min heap.>

Komplexitätsanalyse :

Der Zeitkomplexität dieses Programms ist O(n log n) , Wo N ist die Anzahl der Elemente in der Prioritätswarteschlange.

Der Einfügevorgang hat eine zeitliche Komplexität von O(log n) im schlimmsten Fall, weil die Heap-Eigenschaft beibehalten werden muss. Der Suchvorgang umfasst das Kopieren der Prioritätswarteschlange in eine temporäre Warteschlange und das anschließende Durchlaufen der temporären Warteschlange, was dauert O(n log n) Im schlimmsten Fall dauert dies mehr Zeit, da jedes Element kopiert und aus der Warteschlange entfernt werden muss und die Prioritätswarteschlange für jeden Vorgang neu erstellt werden muss.

Der Raumkomplexität des Programms ist An) weil es speichert N Elemente in der Prioritätswarteschlange und erstellt eine temporäre Warteschlange mit N Elemente.

Anwendungen der Min-Heap-Datenstruktur:

Heap-Sortierung: Min Heap wird als Schlüsselkomponente im Heap-Sortieralgorithmus verwendet, einem effizienten Sortieralgorithmus mit einer Zeitkomplexität von O(nlogn).
Prioritätswarteschlange: Eine Prioritätswarteschlange kann mithilfe einer Min-Heap-Datenstruktur implementiert werden, bei der sich das Element mit dem Mindestwert immer im Stammverzeichnis befindet.
Dijkstras Algorithmus: Im Dijkstra-Algorithmus wird ein Min-Heap verwendet, um die Scheitelpunkte des Diagramms mit dem minimalen Abstand vom Startscheitelpunkt zu speichern. Der Scheitelpunkt mit dem minimalen Abstand liegt immer an der Wurzel des Heaps.
Huffman-Codierung: Bei der Huffman-Codierung wird ein Min-Heap verwendet, um eine Prioritätswarteschlange zu implementieren, um einen optimalen Präfixcode für einen bestimmten Zeichensatz zu erstellen.
K sortierte Arrays zusammenführen: Bei gegebenen K sortierten Arrays können wir sie mithilfe einer Min-Heap-Datenstruktur effizient zu einem einzigen sortierten Array zusammenführen.

Vorteile der Min-Heap-Datenstruktur:

Effizientes Einfügen und Löschen : Min. Heap ermöglicht schnelles Einfügen und Löschen von Elementen mit einer zeitlichen Komplexität von O(log n), wobei n die Anzahl der Elemente im Heap ist.
Effizientes Abrufen des Mindestelements: Das minimale Element in einem Min-Heap befindet sich immer im Stammverzeichnis des Heaps und kann in O(1)-Zeit abgerufen werden.
Platzsparend: Min Heap ist eine kompakte Datenstruktur, die mithilfe eines Arrays oder eines Binärbaums implementiert werden kann, wodurch sie platzsparend ist.
Sortierung: Min. Heap kann verwendet werden, um einen effizienten Sortieralgorithmus wie Heap-Sortierung mit einer zeitlichen Komplexität von O(n log n) zu implementieren.
Prioritätswarteschlange: Min Heap kann verwendet werden, um eine Prioritätswarteschlange zu implementieren, in der das Element mit der minimalen Priorität effizient in O(1)-Zeit abgerufen werden kann.
Vielseitigkeit: Min Heap hat mehrere Anwendungen in der Informatik, darunter Graphalgorithmen, Datenkomprimierung und Datenbanksysteme.

Insgesamt ist Min Heap eine nützliche und vielseitige Datenstruktur, die effiziente Operationen und Platzeffizienz bietet und mehrere Anwendungen in der Informatik bietet.