logo

TechCodeview

Flächenformeln

Flächenformeln Für verschiedene Objekte gibt es Formeln, mit denen die Fläche verschiedener Objekte ermittelt wird. Fläche ist der Raum, der von der Grenze einer beliebigen Figur eingenommen wird. Flächenformeln verschiedener geometrischer Formen hängen von verschiedenen Parametern wie Abmessungen, Höhe und Radius verschiedener geometrischer Formen ab. Es gibt zwei Arten geometrischer Formen:

  • Zweidimensionale Formen (2-D-Formen)
  • Dreidimensionale Formen (3D-Formen)

In diesem Artikel lernen wir die Flächenformeln für verschiedene 2D- und 3D-Formen im Detail kennen, z. B. die Fläche eines Rechtecks, die Fläche eines Quadrats, die Fläche eines Kreises, die Fläche eines Würfels usw. und andere.



Inhaltsverzeichnis

Was ist Fläche?

Der von der Grenze einer Figur eingenommene Raum wird als Fläche der Figur bezeichnet. Es wird im Einheitsquadrat gemessen. Die SI-Einheit zur Messung der Fläche ist m2. Die Fläche wird in verschiedenen mathematischen Konzepten verwendet und wird auch in realen Szenarien verwendet, z. B. um die Fläche eines Raums, eine Flächentabelle usw. zu ermitteln.

Was sind Flächenformeln?

Flächenformeln sind wesentliche Werkzeuge der Mathematik, um den von verschiedenen zweidimensionalen Formen eingeschlossenen Raum zu berechnen. Diese Formeln können verwendet werden, um die geometrische Fläche zu ermitteln Figuren wie Quadrate, Rechtecke, Kreise, Dreiecke, Trapeze und Ellipsen. Mithilfe dieser Formeln können wir die Fläche verschiedener Formen genau berechnen und so reale Probleme lösen und wichtige Berechnungen durchführen.



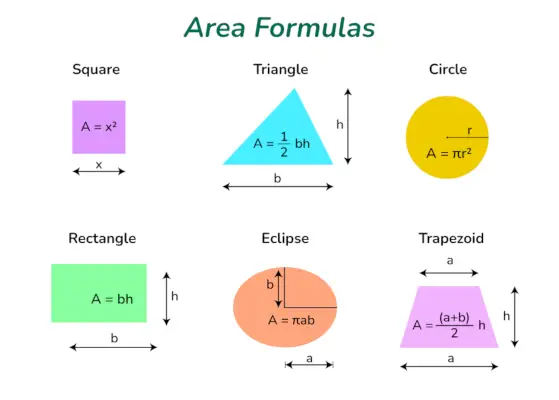
Flächenformeln

Flächenformeln

Was sind 2D-Formen?

Formen, die nur zwei Dimensionen haben, werden als Formen bezeichnet 2D-Formen . Sie werden im 2D-Raum gezeichnet und sind abhängig von 2 Parameter, im Allgemeinen Länge (l) und Breite (b). Die verschiedenen 2D-Formen sind: Rechteck, Quadrat, Dreieck, Kreise und andere.

Flächenformel für 2D-Formen

Formeln für die Fläche von 2D-Formen sind die Formeln, die verwendet werden, um die Fläche der verschiedenen 2D-Formen zu bestimmen, z. B. die Fläche eines Dreiecks, die Fläche eines Quadrats, die Fläche eines Rechtecks, die Fläche einer Raute usw. Diese Flächenformeln werden in der Mathematik häufig verwendet verschiedene geometrische Probleme lösen. Verschiedene Flächenformeln für verschiedene Formen sind:



Flächenformel eines Rechtecks

Rechteck ist eine zweidimensionale Figur Das ist ein Viereck, d. h. es hat vier Seiten, deren gegenüberliegende Seiten parallel und gleich sind. Alle Winkel im Rechteck sind gleich und ihr Maß beträgt 90 Grad. Die Diagonalen des Rechtecks ​​sind gleich und sind senkrechte Winkelhalbierende zueinander.

Die Formel zur Berechnung der Fläche eines Rechtecks ​​lautet mit Länge und l und Breite B Ist,

  • Fläche des Rechtecks ​​(A) = l×b Quadrateinheiten

Flächenformel eines Quadrats

Ein Quadrat ist eine zweidimensionale Figur, die ein Viereck ist, d. h. sie hat vier Seiten, ihre gegenüberliegenden Seiten sind parallel und alle vier Seiten eines Quadrats sind gleich. Alle Winkel im Quadrat sind gleich und ihr Maß beträgt 90 Grad. Die Diagonalen des Quadrats sind gleich und sind senkrechte Winkelhalbierende zueinander.

Die Formel zur Berechnung der Fläche eines Quadrats mit Seite A Ist,

  • Fläche des Quadrats (A) = a 2 Quadrateinheiten

Flächenformel eines Dreiecks

Dreieck ist das einfachste Polygon, das durch die Verbindung dreier gerader Linien entsteht. Wie der Name schon sagt, handelt es sich um ein Polygon mit drei Winkeln. Die Summe der Längen aller Seiten des Dreiecks ist der Umfang des Dreiecks und der Raum innerhalb des Umfangs des Dreiecks ist die Fläche des Dreiecks.

paraphrasieren, wenn von Rudyard Kipling

Die Formel zur Berechnung der Fläche eines Dreiecks mit Basis B ist und Höhe H Ist,

  • Fläche des Dreiecks (A) = 1/2 × bh Quadrateinheiten

Flächenformel eines Kreises

Kreis ist eine geometrische Figur ohne gerade Linie. Es ist der Ort des Punktes, der immer einen konstanten Abstand vom Fixpunkt hat. Der Fixpunkt wird der Mittelpunkt des Kreises genannt und der feste Abstand ist der Radius des Kreises.

Die Formel zur Berechnung der Fläche eines Kreises mit r als Radius des Kreises,

  • Kreisfläche (A) = πr 2 Quadrateinheiten

Flächenformel eines Parallelogramms

Das Parallelogramm ist eine zweidimensionale Figur bei dem die gegenüberliegenden Seiten parallel und gleich sind. Die Formel zur Berechnung der Fläche eines Parallelogramms mit Basis B und Höhe H Sind,

  • Fläche des Parallelogramms (A) = bh Quadrateinheiten

Flächenformel einer Raute

Rhombus ist ein Viereck, bei dem alle vier Seiten gleich und parallel sind, aber nicht alle Winkel gleich sind. Die Formel zur Berechnung der Fläche einer Raute mit einer Diagonale D 1 Und D 2 Sind,

  • Fläche der Raute (A) = 1/2 × d 1 × d 2 Quadrateinheiten

Flächenformel eines Trapezes

Trapezoid ist ein anderer Name für Trapez . Es handelt sich um ein Viereck, bei dem die gegenüberliegenden Seiten parallel sind. Die Formel zur Berechnung der Fläche eines Trapezes mit parallelen Seiten A Und B und Höhe H Ist,

  • Fläche des Trapezes (A) = 1/2(a +b)h Quadrateinheiten

Flächenformel einer Ellipse

Ellipse ist eine zweidimensionale Form und gehört zu den konischen Abschnitten. Die Formel zur Berechnung der Fläche einer Ellipse mit der Achse as A Und B Sind,

  • Fläche der Ellipse (A) = πab Quadrateinheiten

Flächenformel eines Halbkreises

Ein Halbkreis ist eine zweidimensionale Figur, die die Hälfte eines Kreises darstellt. Die Formel zur Berechnung der Fläche eines Halbkreises mit dem Radius r lautet:

  • Fläche des Halbkreises (A) = 1/4(πr 2 ) Quadrateinheiten

Tabelle mit Flächenformeln

Die Formeln für die Flächen der verschiedenen 2D-Figuren sind in der unten hinzugefügten Tabelle aufgeführt.

Figuren

Formel

Variablen

Rechteck

Fläche = l×b
  • l ist die Länge
  • b ist die Breite

Quadrat

Fläche = a2

a ist die Seite des Quadrats

Dreieck

Fläche = 1/2×bh
  • b ist die Basis
  • h ist die Höhe

Kreis

Fläche = πr2

r ist der Radius des Kreises

Trapez

Fläche = 1/2×(a+b)h
  • a ist die erste Basis
  • b ist die zweite Basis

Rhombus

Fläche = 1/2×d1×d2
  • D1ist die Eine Diagonale
  • D2ist die zweite Diagonale

Parallelogramm

Fläche = b × h
  • b ist die Basis
  • h ist die Höhe

Ellipse

Fläche = πab
  • a ist der Radius der Hauptachse
  • b ist der Radius der Nebenachse

Was sind 3D-Formen?

3D-Formen sind Formen, die in 3D-Räumen gezeichnet werden. Sie haben drei Dimensionen, die ihre Parameter sind. Die Fläche dieser Formen hängt von der Länge, Breite und Höhe der 3D-Formen ab. Verschiedene 3D-Formen sind Würfel, Quader, Zylinder, Kegel, Kugel und andere. Die Fläche von 3D-Formen lässt sich in zwei Kategorien einteilen: die gekrümmte Oberfläche (laterale Oberfläche) {CSA} und die Gesamtoberfläche (TSA). Die CSA ist die Fläche aller gekrümmten Oberflächen der 3D-Formen und TSA ist die Fläche aller Flächen der 3D-Formen.

Flächenformel für 3D-Formen

Die Fläche der 3D-Formen ist der Raum, der von allen Gesichtern der Figur eingenommen wird. Es wird in Einheiten gemessen2. Die SI-Einheit der Fläche ist m2. Der Fläche des Würfels , Fläche eines Quaders, Fläche eines Zylinders, Fläche eines Kegels und andere liegen im Bereich der 3D-Formen. Die unten hinzugefügte Tabelle zeigt die Formeln verschiedener 3D-Figuren.

Formbereich

Oberfläche

Parameter

Fläche des Würfels

6a2

a ist die Kantenlänge

Fläche von Quader

2(lb + links + bh)
  • l ist die Kantenlänge
  • b ist die Kantenbreite
  • h ist die Höhe der Kante

Fläche des Kegels

πr(r + l)
  • r = Radius der kreisförmigen Basis
  • l = Schräghöhe

Fläche des Zylinders

2π(r + h)
  • r = Radius der kreisförmigen Basis
  • h = Höhe des Zylinders

Bereich der Kugel

4πr2

r ist der Radius der Kugel

Bereich der Hemisphäre

3πr2

r ist der Radius der Hemisphäre

Fläche eines rechteckigen Prismas

2(wl + hl + hw)
  • l ist die Kantenlänge
  • w ist die Breite der Kante
  • h ist die Höhe der Kante

Überprüfen Sie auch

Java-Array initialisieren
  • Flächen- und Umfangsformeln
  • Oberflächenformeln

Beispiele für Flächenformeln

Beispiel 1: Ermitteln Sie die Fläche eines Rechtecks ​​mit einer Länge von 5 cm und einer Breite von 2 cm.

Lösung:

Gegeben,

  • Länge des Rechtecks ​​(l) = 5 cm
  • Breite des Rechtecks ​​(b) = 2 cm

Fläche des Rechtecks ​​(A) = l × b

A = 5 cm × 2 cm
= 10cm2

Beispiel 2: Finden Sie die Fläche des quadratischen Parks mit einer Seitenlänge von 4 m.

Lösung:

Gegeben,

  • Seite des Quadrats (a) = 4 m

Fläche des Quadrats = a2
= (4)2= 16 m2

Somit beträgt die Fläche des quadratischen Parks 16 m²2

Beispiel 3: Ermitteln Sie die Fläche einer dreieckigen Platte, deren Höhe 6 cm und deren Grundfläche 6 cm beträgt.

Lösung:

Gegeben,

HTML-Listenfeld
  • Höhe des Dreiecks (h) = 6 cm
  • Basis des Dreiecks (b) = 8 cm

Fläche des Dreiecks (A) = 1/2(b × h)

A = 1/2(8 × 6)
= 48/2 = 24 cm2

Die Fläche der dreieckigen Platte beträgt 24 cm2

Beispiel 4: Ermitteln Sie die Fläche einer Kreisscheibe mit einem Radius von 1,4 cm.

Lösung:

Gegeben,

  • Kreisradius (r) = 1,4 cm

Kreisfläche (A) = πr2

A = π(1,4)2
= 22/7(1,4)(1,4) = (4,4)(1,4)
= 6,16 cm2

Die Fläche der Kreisscheibe beträgt 6,16 cm2

Häufig gestellte Fragen zu Flächenformeln

Was sind Flächenformeln?

Die Flächenformeln sind die Formeln, mit denen die Fläche einer beliebigen Figur ermittelt werden kann. Es wird verwendet, um den von der Figur eingenommenen Platz zu ermitteln. Im Allgemeinen wird der Bereich mit dem Buchstaben „A“ dargestellt. und wird in Einheiten gemessen2, also cm2, M2, usw.

Was ist die Flächenformel für ein Quadrat?

Die Flächenformel für ein Quadrat ist die Formel zur Berechnung der vom Quadrat eingenommenen Fläche. Die Formel zur Berechnung der Fläche des Quadrats lautet:

Fläche des Quadrats = (Seite) 2

Was ist die Flächenformel für ein Rechteck?

Die Flächenformel für ein Rechteck ist die Formel zur Berechnung des vom Rechteck eingenommenen Raums. Die Formel zur Berechnung der Fläche des Rechtecks ​​lautet:

Fläche des Rechtecks ​​= Länge × Breite

Was ist die Flächenformel für ein Dreieck?

Die Flächenformel für ein Dreieck ist die Formel zur Berechnung des vom Dreieck eingenommenen Raums. Die Formel zur Berechnung der Fläche des Dreiecks lautet:

Fläche des Dreiecks = 1/2 (Basis × Höhe)

Was ist die Flächenformel für einen Kreis?

Die Flächenformel für einen Kreis ist die Formel zur Berechnung des vom Kreis eingenommenen Raums. Die Formel zur Berechnung der Kreisfläche lautet:

Kreisfläche = π(Radius) 2

Was ist die Flächenformel für ein Viereck?

Formel zur Berechnung der Fläche eines Vierecks,

Fläche des Vierecks = 1/2 × Diagonale 1 × Diagonale 2

Was ist die Flächenformel eines Dreiecksprismas?

Die Formel für die Fläche des Dreiecksprismas lautet:

Fläche des dreieckigen Prismas = (Umfang der Basis × Länge des Prismas) + 2 × Grundfläche

Was ist die Flächenformel eines Polygons?

Die Formel zur Berechnung der Polygonfläche lautet:

Fläche des Polygons = 1/2 × (Umfang × Apothem)

Was ist die Flächenformel eines rechtwinkligen Dreiecks?

Die Formel für die Fläche eines rechtwinkligen Dreiecks lautet:

Fläche des rechtwinkligen Dreiecks = 1/2 × Senkrechte × Basis

Was ist die Flächenformel des Pentagons?

Die Formel für die Fläche des Pentagons lautet:

Fläche des Pentagons = 1/2 × Umfang × Apothem