Die Kosinusfunktion oder der cos Funktion ist kurz gesagt eine der sechs Trigonometrische Funktionen grundlegend für die Trigonometrie. Der Kosinus wird in der Trigonometrie als das Verhältnis der Basis zur Hypotenuse eines rechtwinkligen Dreiecks angegeben. Die Kosinusfunktion wird als Cos x dargestellt, wobei x der Winkel ist, für den das Kosinusverhältnis berechnet wird. In Bezug auf die Funktion können wir sagen, dass x die Eingabe oder der Definitionsbereich der Kosinusfunktion ist.

Es wird häufig in einer Vielzahl von Fächern wie Physik, Geometrie und Ingenieurwesen eingesetzt, unter anderem aufgrund seiner periodischen Natur. Beispielsweise wird es zur Definition der Wellennatur von Schallwellen, zur Berechnung des elektrischen Flusses durch eine ebene Fläche usw. verwendet. In diesem Artikel erfahren wir im Detail, was die Kosinusfunktion ist Domäne und Bereich der Kosinusfunktion, der Periode und dem Graphen der Kosinusfunktion.

Inhaltsverzeichnis

• Was ist die Kosinusfunktion?
• Cos im Einheitskreis
• Cosinus-Funktionsgraph
• Umkehrung der Kosinusfunktion
• Kosinusfunktion in der Analysis
• Cos-Funktionsidentitäten

Was ist die Kosinusfunktion?

Die Kosinusfunktion ist eine trigonometrische Funktion, die grundsätzlich periodischer Natur ist. Die Kosinusfunktion wird als cos x ausgedrückt, wobei x einer der spitzen Winkel eines rechtwinkligen Dreiecks ist. Die Kosinusfunktion ermittelt das Verhältnis von Basis und Hypotenuse für einen gegebenen Wert von x. Die Kosinusfunktion wird als cos(x) oder cos(θ) abgekürzt, wobei x der Winkel im Bogenmaß und Theta θ der Winkel im Bogenmaß ist Grad allgemein. Die Kosinusfunktion kann mithilfe eines Einheitskreises definiert werden, d. h. eines Kreises mit Einheitsradius, wie wir später in diesem Artikel sehen werden. Es ist periodischer Natur und wiederholt seine Werte nach jeder vollständigen Winkeldrehung. Auf einer kartesischen Ebene kann man sie als Vektorkomponente der Hypotenuse parallel zur x-Achse bezeichnen.

Definition der Kosinusfunktion

Die Kosinusfunktion ist in einem rechtwinkligen Dreieck definiert als das Verhältnis der Länge der Seite, die an den betreffenden Winkel angrenzt, zur Länge der Hypotenuse. Mathematisch ist die Kosinusfunktion gegeben als

Cos x = Cos θ = Länge der Basis/Länge der Hypotenuse = b/h = OB/OA

Wo X ist der Winkel im Bogenmaß und θ ist der entsprechende Winkel in Grad.

Bereich und Bereich der Cos-Funktion

Wir wissen, dass für eine Funktion die Domäne die zulässigen Eingabewerte und der Bereich der Ausgabewert für diesen bestimmten Eingabe- oder Domänenwert ist. Daher können wir davon ausgehen, dass eine Funktion wie ein Prozessor fungiert, der Eingaben entgegennimmt, verarbeitet und bestimmte Ausgaben ausgibt. Der Bereich und Bereich der Cos-Funktion wird im Folgenden erläutert:

• Bereich der Kosinusfunktion: R d.h. Menge aller reellen Zahlen.
• Bereich der Kosinusfunktion: [-1, 1], d. h. die Ausgabe variiert zwischen allen reellen Zahlen zwischen -1 und 1.

Periode einer Kosinusfunktion

Der Funktion ist periodischer Natur, d. h. es wiederholt sich nach 2π oder 360°. Mit anderen Worten, es wiederholt sich nach jeder vollständigen Umdrehung. Daher ist die Periode der Kosinusfunktion eine vollständige Drehung oder ein Winkel von 360° (oder 2π).

Kehrwert einer Kosinusfunktion

Der Kehrwert einer Kosinusfunktion ist bekannt als Sekante Funktion bzw Sek kurz gesagt. Mathematisch ist der Kehrwert der Kosinusfunktion gegeben als

Lineare Suche in Java

Sek(θ) = 1/cos(θ)

Gemäß den Regeln von Gegenseitigkeiten , wenn wir den Cos x mit Sec x multiplizieren, ist das Produkt immer 1.

Cosinus-Funktionsgraph

Der Graph der Kosinusfunktion ähnelt dem Graphen der Sinusfunktion mit dem grundlegenden Unterschied, dass für x = 0 der Sinusfunktionsgraph vom Ursprung ausgeht, während bei x = 0 der Kosinusfunktionsgraph von (0, 1) bei y-aixs verläuft. Es folgt die Grafik des Wertes der Kosinusfunktion, d. h. y = cos x

Die oben besprochenen Eigenschaften sind im Diagramm zu sehen, wie zum Beispiel die periodische Natur der Funktion.

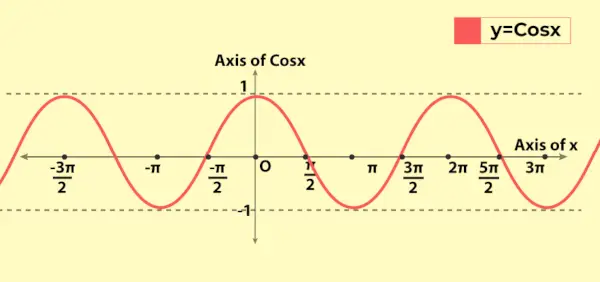
Variation der Kosinusfunktion im Diagramm

Da der Bereich der Kosinusfunktion [-1, 1] beträgt, variiert er im Diagramm von -1 bis 1. Es zeigt seine periodische Natur, da sich der Graph nach jeder Länge 2π auf der x-Achse wiederholt. Dies spiegelt wider, dass die Kosinusfunktion eine Periode von 2π (oder 360°) hat.

Cos im Einheitskreis

Die Kosinusfunktion kann mithilfe des Einheitskreises definiert werden. Lassen Sie uns verstehen, wie wir die Kosinusfunktion anhand des Einheitskreises definieren können.

Betrachten Sie ein Liniensegment OA, das sich um den Punkt O dreht, wobei O der Ursprung der kartesischen Ebene ist. Somit beschreibt die Drehung von OA einen Einheitskreis (Kreis mit Einheitsradius), der im Ursprung O zentriert ist und der Punkt A immer auf diesem Kreis liegt. Wenn wir eine Senkrechte von A auf die x-Achse fallen lassen und den Schnittpunkt B nennen und θ der Winkel ist, den OA mit der positiven Richtung der x-Achse bildet, dann ist cos(θ) = Projektion der Hypotenuse auf x -axis = OB/|OA| = OB (da |OA| = 1 Einheit).

Beachten Sie, dass die Richtung OB wichtig ist, wie in den folgenden Abbildungen dargestellt. Das grüne Segment gibt die Länge/Größe an und der Pfeil gibt die Richtung (+ve oder -ve) von cos(θ) an.

Beachten Sie, dass der Wert von cos(θ) für θ, das zum ersten und vierten Quadranten gehört, positiv ist, während er für θ, das zum zweiten und dritten Quadranten gehört, negativ ist.

Umkehrung der Kosinusfunktion

Die Umkehrung einer Kosinusfunktion, bekannt als Arkuskosinus Funktion und abgekürzt als arccos(x) oder cos ^-1 (X) ist wie folgt definiert

cos(x) = y

⇒ cos ^-1 (y) = x

Bereich und Bereich der Umkehrkosinusfunktion

Der Bereich und der Bereich der Umkehrkosinusfunktion sind unten aufgeführt:

• Bereich der Umkehrkosinusfunktion: Alle reellen Zahlen im Bereich [-1, 1]
• Bereich der Umkehrkosinusfunktion: Alle reellen Zahlen im Bereich [0, π]

Hyperbolische Kosinusfunktion

Hyperbolische Funktionen sind ein analoges Äquivalent der trigonometrischen Funktion, deren algebraischer Ausdruck in Form einer Exponentialfunktion erfolgt. Die hyperbolische Kosinusfunktion wird abgekürzt als cosh(x) Wo X ist ein hyperbolischer Winkel ein Konzept der hyperbolischen Geometrie. So wie (cos(x), sin(x)) einen Punkt auf einem Einheitskreis darstellt, stellt (cosh(x), sinh(x)) einen Punkt auf einer Einheitshyperbel dar, d. h. xy = 1, wobei sinh(x) eine Hyperbel darstellt Sinusfunktion. Die algebraische Entwicklung der hyperbolischen Kosinusfunktion wird wie folgt angegeben:

cosh(x) = (z ^X + und ^-X )/2

Weitere Einzelheiten zu hyperbolischen Funktionen würden den Rahmen dieses Artikels sprengen, Sie können jedoch darauf verweisen Dieser Artikel .

Kosinusfunktion in der Analysis

Der Zweig der Infinitesimalrechnung in der Mathematik befasst sich mit der Differenzierung und Integration einer gegebenen Funktion. Die Differenzierung einer Funktion ist die Änderungsrate der Funktion in Bezug auf die unabhängige Variable, während die Integration der umgekehrte Prozess der Differenzierung ist, bei dem es darum geht, das Integral einer Funktion zu finden, deren Ableitung existiert.

Ableitung der Kosinusfunktion

Der Derivat der Kosinusfunktion ist gleich dem Negativ der Sinusfunktion. Mathematisch

d(cos(x))/dx = -sin(x)

Integration der Kosinusfunktion

Der unbestimmtes Integral Die Kosinusfunktion ist gleich der Sinusfunktion. Mathematisch –

∫cos(x)dx = sin(x) + C, wobei C die Integrationskonstante ist.

Sinus- und Kosinusfunktionen

Die folgende Grafik stellt den Hauptunterschied zwischen Sinus- und Kosinusfunktion dar:

Unterschied zwischen Sinus- und Kosinusfunktionen

Die folgende Tabelle listet die Unterschiede zwischen Sinus- und Kosinusfunktion auf:

Cos-Werttabelle

Die folgende Tabelle enthält die Werte der Kosinusfunktion für einige häufig vorkommende Winkel im ersten Quadranten der kartesischen Ebene:

Wir können die Werte anderer üblicher Winkel wie 15°, 75°, 195°, -15° usw. leicht berechnen, indem wir diese Werte verwenden, indem wir die Formeln cos (x + y) und cos (x – y) verwenden, die später in diesem Dokument beschrieben werden Artikel.

Überprüfen, Trigonometrische Tabelle

Cos-Funktionsidentitäten

Die grundlegenden trigonometrischen Identitäten im Zusammenhang mit der Kosinusfunktion sind unten aufgeführt:

• ohne²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/sek(x)
• cos 2x = cos²x – Sünde²x = 1 – 2sin²x = 2cos²x – 1 = (1 – tan²x/1 + tan²X)
• cos 3x = 4cos³x – 3cos x

In Verbindung stehende Artikel

• Differenzierung trigonometrischer Funktionen
• Inverse trigonometrische Funktionen
• Inverse trigonometrische Ableitungen

Gelöste Beispiele zur Kosinusfunktion

Hier sind einige gelöste Beispiele, die Ihnen helfen, das Konzept der Kosinusfunktion besser zu verstehen.

Beispiel 1: Was sind die Maximal- und Minimalwerte der Kosinusfunktion?

Lösung:

Der Maximalwert der Kosinusfunktion beträgt 1 bei 0° und 180°, während der Minimalwert der Funktion -1 bei 180° beträgt.

Beispiel 2: Bei welchen Winkeln im Bereich [0, 360] ist der Wert der Kosinusfunktion 0?

Lösung:

Der Wert der Kosinusfunktion beträgt 0 bei den Winkeln 90° und 270°.

Beispiel 3: Für welche Quadranten ist der Wert der Kosinusfunktion negativ?

Lösung:

Die Kosinusfunktion ist im II negativ^ndund III^rdQuadranten.

Beispiel 4: Berechnen Sie den Wert von cos (45°).

Lösung:

So ermitteln Sie die Monitorgröße

Gemäß der oben angegebenen Identität 4 gilt cos(-x) = cos(x).

Daher ist cos(-45°) = cos(45°) = 1/√2

Beispiel 5: Berechnen Sie den Wert von cos(15°).

Lösung:

Unter Verwendung der oben angegebenen Identität 3 –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Beispiel 6: Was ist cos ^-1 (1/2) im Bereich [0,π]?

Lösung:

Lass es sein^-1(1/2) = y.

Daher ist cos(y) = 1/2 ⇒ y = π/3 im oben angegebenen Bereich.

Daher lautet die Antwort π/3.

Beispiel 7: Welchen Wert hat cos(-15°)?

Lösung:

Unter Verwendung der oben angegebenen Identität 3 –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternativ können wir auch die Identität cos(-x) = cos(x) verwenden und den in Beispiel 5 berechneten Wert von cos(15°) verwenden.

Beispiel 8: Berechnen Sie die Fläche unter dem Graphen der Kosinusfunktion für x = 0 bis x = π/2.

Lösung:

Die gegebene Fläche kann durch Lösen des folgenden bestimmten Integrals berechnet werden:

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Daher lautet die Antwort 1 Einheitsquadrat.

Beispiel 9: Wenn cos(x) = π/3, ermitteln Sie den Wert von cos(3x) (in Dezimalform mit einer Genauigkeit von zwei Dezimalstellen).

Lösung:

Unter Verwendung der Identität – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Beispiel 10: Ermitteln Sie den Wert von cos(120°).

Lösung:

Verwendung der Identität für cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Übungsfragen: Cos-Funktionen

Q1. Wie lautet die Formel zur Berechnung des Cos eines Winkels in einem rechtwinkligen Dreieck?

Q2. Was ist die geometrische Interpretation des Kosinus auf der kartesischen Ebene?

Q3. Berechnen Sie den Wert von cos(120°).

Q4. Finden Sie den Wert von cos ^-1 (√3/2) im Bereich [π, 2π].

F5. Wenn ein Pfahl einen Schatten gleicher Länge auf den Boden wirft, ermitteln Sie den Winkel der Sonne zum Boden, wenn die Sonne in östlicher Richtung steht.

Zusammenfassung – Kosinusfunktion

Die Kosinusfunktion, bezeichnet als cos(x), ist eine grundlegende trigonometrische Funktion, die als das Verhältnis der Basis zur Hypotenuse in einem rechtwinkligen Dreieck definiert ist und aufgrund ihrer periodischen Natur in verschiedenen Bereichen wie Physik, Technik und Geometrie von wesentlicher Bedeutung ist , das maßgeblich zur Modellierung des Wellenverhaltens beiträgt. Es hat einen Bereich aller reellen Zahlen und einen Bereich von -1 bis 1 und wiederholt seinen Zyklus alle 2 Pi Bogenmaß oder 360 Grad, erkennbar an der wellenförmigen Grafik, die bei (0,1) beginnt. In Bezug auf die Analysis ist die Ableitung von cos(x) − sin( X ), und sein Integral ergibt sin( X )+ C , mit C als Integrationskonstante. Diese Funktion erstreckt sich auch auf hyperbolische Formen wie cosh(x) und verbessert so ihre Anwendung in verschiedenen mathematischen Kontexten und Lösungen, einschließlich Wellenberechnungen und Schwingungen in physikalischen Systemen.

Kosinusfunktion: FAQs

1. Was ist die Kosinusfunktion?

Die Kosinusfunktion ist eine der grundlegenden trigonometrischen Funktionen. Sie ist in einem rechtwinkligen Dreieck definiert als das Verhältnis der Länge der Seite, die an den betreffenden Winkel angrenzt, zur Länge der Hypotenuse.

2. Sind Kosinus und Kosinus in der Trigonometrie gleich?

Ja. cos ist eine Abkürzung/Kurzform der Kosinusfunktion.

3. Was ist der Bereich der Cos-Funktion?

Der Bereich des Kosinus oder der Kosinusfunktion umfasst alle reellen Zahlen im Bereich von -1 bis 1, d. h. [-1,1].

4. Was ist der Bereich der Cos-Funktion?

Der Definitionsbereich des Kosinus oder der Kosinusfunktion ist der Ser aller reellen Zahlen, d. h. R .

5. Was ist der Maximalwert der Kosinusfunktion?

Der Maximalwert der Kosinusfunktion beträgt 1 für alle Winkel, die 0° oder 360° entsprechen.

6. Was ist der Minimalwert der Kosinusfunktion?

Der Mindestwert der Kosinusfunktion beträgt -1 für alle Winkel, die 180° entsprechen.

7. Wie finde ich den Wert von Cos(-x)?

Der Wert von cos(-x) kann berechnet werden, indem der Wert von cos(x) aufgrund der Existenz der folgenden Identität berechnet wird: cos(-x) = cos(x).

8. Wie zeichnet man eine Kosinusfunktion grafisch auf?

Um den Graphen der Kosinusfunktion auf einer kartesischen Ebene zu zeichnen, beziehen Sie sich auf die x-Achse als Darstellung der Winkel im Bogenmaß (oder Grad) und die y-Achse als Darstellung der Werte der Kosinusfunktion für den entsprechenden Winkel auf der x-Achse. Jetzt,

• Schritt 1: Nehmen Sie eine Teilmenge der x-Achse, für die Sie das Diagramm zeichnen möchten.
• Schritt 2: Teilen Sie die x-Achse in diesem Bereich in äquidistante Punkte auf (d. h. zwischen allen Unterpunkten ist der gleiche Abstand). Beachten Sie, dass die Genauigkeit des resultierenden Diagramms umso höher ist, je größer die Anzahl der Unterteilungen ist.
• Schritt 3: Markieren Sie für jeden dieser Unterpunkte x den Punkt (x, cos(x)) im Diagramm.
• Schritt 4: Verbinden Sie alle markierten Punkte, um den Graphen der Kosinusfunktion zu erhalten (für die von Ihnen ausgewählte Teilmenge der x-Achse).

9. Wie finde ich die Periode einer Kosinusfunktion?

Die Periode einer Kosinusfunktion bezieht sich auf den minimalen Wertebereich, nach dem sich die Funktion zu wiederholen beginnt. Wir wissen, dass sich die Kosinusfunktion nach jeder vollständigen Drehung wiederholt, also 2π im Bogenmaß. Daher beträgt die Periode der Kosinusfunktion 2π im Bogenmaß oder 360°.

10. Was ist die Amplitude einer Kosinusfunktion?

Die Amplitude einer Kosinusfunktion bezieht sich auf die maximale Verschiebung des Werts der Funktion von der Mittelposition, d. h. der x-Achse. Die Amplitude der Kosinusfunktion beträgt 1, da die maximale Verschiebung 1 beträgt (für die Werte -1 und 1 bei 180 bzw. 0 Grad). Beachten Sie, dass der Bereich der Kosinusfunktion [-amplitude, Amplitude] beträgt.