A Funktion In der Mathematik handelt es sich um eine spezielle Beziehung zwischen der Menge der Eingabewerte und der Menge der Ausgabewerte. In der Funktion gibt jeder Eingabewert einen bestimmten Ausgabewert an. Wir stellen eine Funktion in der Mathematik dar als y = f(x), wobei X ist der Eingabewert und für jeden X wir erhalten einen Ausgabewert als y.

In diesem Artikel erfahren wir mehr über Folgendes: Funktionen in der Mathematik, ihre verschiedenen Typen, Beispiele und andere im Detail.

Inhaltsverzeichnis

• Was ist eine Funktion in der Mathematik?
• Funktionsdefinition in der Mathematik
• Funktionsbeispiele
• Bedingung für eine Funktion
• Darstellung von Funktionen in der Mathematik
• Identifizierung der Funktion
• Arten von Funktionen
• Was ist eine Funktion in der Algebra?
• Domäne und Bereich einer Funktion
• Zusammensetzung der Funktionen
• Algebra der Funktionen
• Was ist eine Funktion in einem Diagramm?
• Grafikfunktionen
• Gemeinsame Funktionen
• Anwendungen von Funktionen
• Beispiele zur Funktion
• Üben Sie Aufgaben zum Thema „Was ist eine Funktion?“.

Was ist eine Funktion in der Mathematik?

Eine Funktion in der Mathematik ist a Beziehung zwischen den Eingabewerten (Domäne) und den Ausgabewerten (Bereich) der gegebenen Mengen, sodass keine zwei Variablen aus den Domänenmengen mit derselben Variablen in der Bereichsmenge verknüpft sind. Ein einfaches Beispiel für eine Funktion in der Mathematik ist f(x) = 2x, die auf R→R definiert ist. Hier bezieht sich jede Variable in der Domäne nur auf eine Variable im Bereich.

Eine Funktion in der Mathematik hat einen Bereich, einen Kobereich und einen Bereich. Der Definitionsbereich ist die Menge aller möglichen Werte von x und der Bereich der Funktion ist die Menge aller Ausgabewerte von y. Der Bereich ist die Teilmenge der Codomäne einer Funktion. Wir können auch sagen, dass eine Funktion in der Mathematik eine Beziehung mit einer eindeutigen Ausgabe ist und dass keine zwei Eingabewerte in einer Funktion eine ähnliche Ausgabe haben, was bei einer Beziehung der Fall ist.

Funktionsdefinition in der Mathematik

Eine Funktion ist eine spezielle Beziehung oder Methode, die jedes Mitglied der Menge A über eine definierte Beziehung mit einem eindeutigen Mitglied der Menge B verbindet. Menge A wird als Definitionsbereich und Menge B als Co-Domäne der Funktion bezeichnet. Eine Funktion in der Mathematik von Menge A zu Menge B ist definiert als:

f = ∀ a ∈ A, b ∈ B

Jede Funktion ist eine Relation, aber jede Relation ist keine Funktion. Die Kriterien dafür, dass jede Beziehung als Funktion betrachtet wird, da in der Funktion jedes Element der Menge A nur ein Bild in der Menge B hat, während in der Beziehung ein Element der Menge A mehr als ein Bild in der Menge B haben kann.

Wir definieren eine Funktion in der Mathematik von der nichtleeren Menge A zur nichtleeren Menge B, sodass:

(a, b) ∈ f, dann ist f(a) = b

wo wir angerufen haben B als das Bild von A unter der Relation definiert F .

Jedes Element 'A' von Menge A hat ein eindeutiges Bild‘ B ‘ in Menge B dann ist es eine Funktion.

Funktionsbeispiele

Eine Funktion in der Mathematik f ist definiert als y = f(x), wobei X ist der Eingabewert, und für jeden Eingabewert von x erhalten wir einen eindeutigen Wert von y. Verschiedene Beispiele für die auf R→R definierten Funktionen in der Mathematik sind:

String-Verkettung Java

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 usw

Bedingung für eine Funktion

Für zwei beliebige nichtleere Mengen A und B eine Funktion f: A→B bezeichnet das F ist eine Funktion von A nach B, wobei A ist eine Domäne und B ist eine Co-Domain.

Für jedes Element, a ∈ A, gibt es ein eindeutiges Element, b ∈ B, so dass (a,b) ∈ f. Das eindeutige Element b, das mit a zusammenhängt, wird mit f(a) bezeichnet und als f von a gelesen. Dies kann anhand des folgenden Bildes besser verstanden werden:

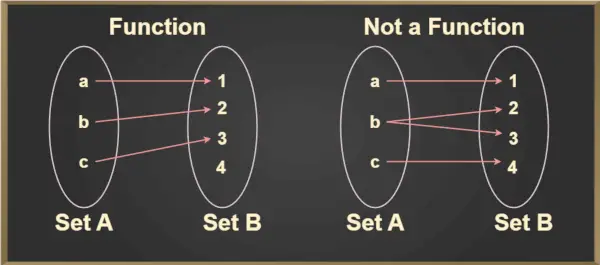
Vertikaler Linientest

Der vertikale Linientest wird verwendet, um festzustellen, ob eine Kurve eine Funktion ist oder nicht. Wenn eine Kurve eine vertikale Linie an mehr als einem Punkt schneidet, ist die Kurve keine Funktion.

Darstellung von Funktionen in der Mathematik

Wir stellen eine Funktion in der Mathematik dar als:

y = f(x) = x + 3

Dabei ist die Menge der Werte von x der Bereich der Funktion und die Menge der Ausgabewerte von y der Co-Bereich der Funktion. Hier ist die Funktion für alle reellen Zahlen definiert, da sie für jedes x einen eindeutigen Wert liefert. Es ist jedoch nicht immer möglich, die Ausgabe für jeden Wert von x zu erhalten. In einem solchen Fall definieren wir die Funktion in zwei Teilen. Dies kann so verstanden werden

• f(x) = 1/(x – 2), wobei x ≠ 2
• f(x) = x²wobei x ∈ {R}

Wir können eine Funktion in der Mathematik als eine Maschine definieren, die einige Eingaben entgegennimmt und eine eindeutige Ausgabe liefert. Die Funktion f(x) = x²wird im Folgenden definiert als:

Wir können eine Funktion in der Mathematik durch die drei Methoden darstellen als:

• Satz geordneter Paare
• Tabellenform
• Grafische Form

Wenn wir beispielsweise eine Funktion darstellen als f(x) = x³

Eine andere Möglichkeit, dieselbe Funktion darzustellen, ist als Menge geordneter Paare als,

f = {(1,1), (2,8), (3,27)}

In der oben genannten Menge ist der Definitionsbereich der Funktion D = {1, 2, 3} und der Bereich der Funktion ist R = {1, 8, 27}

Identifizierung der Funktion

Funktionen werden in der Mathematik als eine besondere Art von Beziehung klassifiziert. Es gibt folgende Regeln, die zur Identifizierung einer Funktion verwendet werden können:

• Eine Beziehung, bei der jede Eingabe einer eindeutigen Ausgabe zugeordnet ist, ist eine Funktion. Dies rief eine Eins-zu-Eins-Funktion hervor.
• Eine Beziehung, bei der zwei Eingaben (Vorbilder) einer einzelnen Ausgabe zugeordnet werden, ist ebenfalls eine Funktion. Dies ist eine Viele-zu-Eins-Funktion.
• Eine Beziehung, bei der einer Eingabe zwei verschiedene Ausgaben zugeordnet werden, ist keine Funktion.
• Eine Beziehung, bei der viele Eingaben vielen Ausgaben nach keiner bestimmten Regel zugeordnet werden, ist keine Funktion.

Arten von Funktionen

Anders Arten von Funktionen werden verwendet, um verschiedene Arten mathematischer Probleme zu lösen, insbesondere im Zusammenhang mit Kurven und Gleichungen. In der Mathematik gibt es drei Haupttypfunktionen, die auf der Elementzuordnung von Menge A zu Menge B basieren.

Injektionsfunktion oder Eins-zu-Eins-Funktion

Die Funktion, bei der jedes Element der Domäne ein eindeutiges Bild in der Codomäne hat, wird als Funktion bezeichnet Injektiv oder Eins-zu-Eins-Funktion .

f: A → B heißt eins zu eins oder injektiv, wenn die Bilder verschiedener Elemente von A unter f verschieden sind, d. h.

Fa ₁ ) = b ₁ , f(a ₂ ) = b ₂

wo ein₁, A₂∈ A und b₁, B₂∈ B

Surjektive Funktionen oder Onto-Funktion

Surjektive Funktion ist die Funktion, bei der jedes Element der Codomäne ein Vorbild in der Domäne hat. Es heißt auch Auf die Funktion Das bedeutet, dass jedes Element der Codomäne jedem Element der Domäne zugeordnet ist. Kein Element der Codomain sollte eine leere Beziehung haben. Die Anzahl der Elemente von Codomain und Range ist gleich.

f: A → B heißt on, wenn jedes Element von B das Bild eines Elements von A unter f ist, d. h. für jedes b ϵ B existiert ein Element 'a' in A, so dass f(a) = b.

Bijektive Funktion

Wenn eine Funktion sowohl Eigenschaften des Injektiven (Eins zu Eins) als auch des Surjektiven (Auf-Funktion) hat, heißt die Funktion a Bijektive Funktion . In der bijektiven Funktion ist jedes Element der Domäne mit jedem Element der Codomäne verknüpft und es besteht auch eine Eins-zu-eins-Beziehung. Dies impliziert, dass die Anzahl der Elemente der Kodomäne und des Bereichs gleich ist und kein Element in der Domäne oder Kodomäne eine leere Beziehung hat.

Basierend auf den Ausgabewerten werden die Funktionen in ungerade und gerade Funktionen klassifiziert. Werfen wir einen Blick darauf

Seltsame Funktionen

Eine ungerade Funktion ist ein Funktionstyp, der eine Symmetrie zum Ursprung aufweist. Insbesondere wenn f(x) eine ungerade Funktion ist, gilt: f(-x) = -f(x)

Gleiche Funktion

Eine gerade Funktion ist ein Funktionstyp, der eine Symmetrie um die y-Achse aufweist. Insbesondere wenn f(x) eine gerade Funktion ist, gilt: f(-x) = f(x)

Was ist eine Funktion in der Algebra?

Eine Funktion in Algebra ist eine Gleichung, für die jedes x, das in die Gleichung eingesetzt werden kann, genau eine Ausgabe wie z. B. y aus der Gleichung erzeugt. Es wird als y = f(x) dargestellt, wobei x eine unabhängige Variable und y eine abhängige Variable ist.

Zum Beispiel:

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Domäne und Bereich einer Funktion

Domäne und Bereich einer Funktion sind Eingabe- bzw. Ausgabewerte einer Funktion. Nehmen wir zum Beispiel an, wir haben eine Funktion mit der Formel f(x) = x². Hier können wir alle reellen Zahlen als Eingabewert von x verwenden und die Ausgabe wird immer eine positive reelle Zahl sein. Daher besteht sein Bereich aus allen reellen Zahlen, die als R dargestellt werden, während sein Bereich aus einer Menge positiver reeller Zahlen besteht, die als R dargestellt werden⁺

Zusammensetzung der Funktionen

Wenn f: A → B und g: B → C zwei Funktionen sind. Dann wird die Zusammensetzung von f und g als f(g) bezeichnet und als Funktion definiert Nebel = f(g(x)) für x ∈ A.

Nehmen wir zwei Funktionen f(x) = x + 3 und g(x) = 2x²

Nebel = f(g(x))

⇒ Nebel = f(2x²)

⇒ Zahn = 2x²+ 3

Erfahren Sie mehr, Zusammensetzung der Funktion

Algebra der Funktionen

Die Algebra der Funktionen umfasst die algebraischen Operationen, die zwischen zwei Funktionen ausgeführt werden. Die algebraische Operation für zwei Funktionen f(x) und g(x), die auf dem reellen Wert von x definiert sind, wird unten erwähnt:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Denn k ist eine reelle Zahl}
• (f/g)(x) = f(x) /g(x); {Für g(x) ≠ 0}

Was ist eine Funktion in einem Diagramm?

Eine Funktion lässt sich leicht in einem Diagramm darstellen. Jede Funktion im Diagramm stellt eine Kurve (einschließlich einer geraden Linie) in der x-y-Ebene dar, die ihren Eingabe- und entsprechenden Ausgabewerten zugeordnet ist.

Um eine Funktion auf einem Diagramm darzustellen, suchen Sie zunächst einige Punkte, die auf der Funktion liegen, und verbinden Sie diese Punkte dann entsprechend dem Ort der Funktion. Um beispielsweise die Funktion (gerade) f(x) = y = 5x – 2 grafisch darzustellen, benötigen wir einen Punkt im Diagramm. Um den Punkt im Diagramm zu finden, nehmen wir zunächst die zufälligen Werte von x und ermitteln dann die entsprechenden Werte von y, wie folgt:

f(x) = y = 5x- 2

wenn x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

wenn x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

wenn x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Wenn wir nun diese Punkte verbinden, können wir den Graphen der Funktion y = 5x – 2 erhalten

Grafikfunktionen

Wenn man die Werte von x kennt, kann man eine Funktion f(x) in einem Diagramm darstellen. Da y = f(x), können wir den zugehörigen Wert für y ermitteln, indem wir mit den Werten von x beginnen. Als Ergebnis können wir einen Graphen in einer Koordinatenebene mit x- und y-Werten zeichnen. Stellen Sie sich das folgende Szenario vor:

Angenommen, y = x + 3

Wenn x = 0, y = 3

Ähnlich,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Als Ergebnis können wir mit diesen Werten den Graphen für die Funktion x + 3 zeichnen.

Gemeinsame Funktionen

Einige häufig in der Mathematik verwendete Funktionen werden im Folgenden erläutert:

Echte Funktion

Echte Funktion bezieht sich in der Mathematik auf eine Funktion, deren Domäne und Bereich Teilmengen der reellen Zahlen sind (bezeichnet als ℝ). Einfacher ausgedrückt ist eine reelle Funktion eine mathematische Regel oder Beziehung, die jeder reellen Zahleneingabe einen reellen Zahlenwert zuweist.

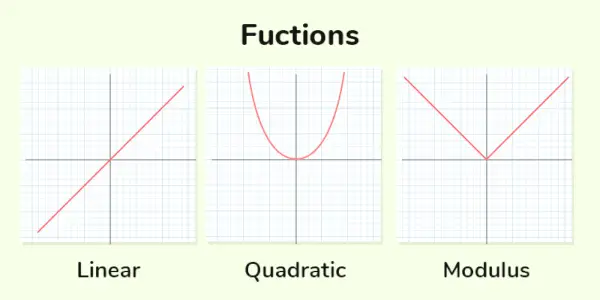
Echte Funktionen

Polynomfunktion

Die Funktion, in der die Exponenten algebraischer Variablen nicht negative ganze Zahlen sind, heißt a Polynomfunktion . Wenn die Potenz der Variablen 1 ist, spricht man von einer linearen Funktion, wenn die Potenz 2 ist, spricht man von einer quadratischen Funktion, und wenn die Potenz 3 ist, spricht man von einer kubischen Funktion. Nachfolgend sind einige Beispiele für Polynomfunktionen aufgeführt:

• y = x²
• y = 2x + 3
• y = 3x³

Polynomfunktionen können weiter in folgende Typen eingeteilt werden:

Lineare Funktion : Lineare Funktionen sind diejenigen, bei denen die maximale Potenz der Variablen 1 ist. Die allgemeine Form von Lineare Funktion Ist y = mx + c

Quadratische Funktion : Quadratische Funktionen sind solche, bei denen die maximale Potenz der Variablen 2 beträgt. Allgemeine Form von quadratische Funktion Ist, Axt ² + bx + c = 0

Kubische Funktion : Kubische Funktion sind solche, bei denen die maximale Potenz der Variablen 3 beträgt. Die allgemeine Form der kubischen Funktion wird angegeben als Axt ³ + bx ² + cx + d = 0

Umkehrfunktion

Umkehrfunktion ist die Funktion, die die Umkehrung einer anderen Funktion enthält. Nehmen wir an, wir haben eine Funktion y = f(x), dann ist ihre Umkehrfunktion x = f^-1(y). In y = f(x) ist die Domäne x und der Bereich ist y, während im Fall von x = f^-1(y), die Domäne ist y und der Bereich ist x. Somit können wir sagen, dass der Bereich der ursprünglichen Funktion der Bereich ihrer Umkehrfunktion ist und der Bereich der ursprünglichen Funktion der Bereich der ursprünglichen Funktion ist. Einige Beispiele für Umkehrfunktionen sind:

atoi c

• y = also^-1(X)
• y = x^-1

Flächenfunktion

Die Flächenfunktion bezieht sich typischerweise auf eine mathematische Funktion, die die Fläche einer geometrischen Form oder Region berechnet. Die Flächenfunktion verwendet einen oder mehrere Parameter als Eingabe und gibt die Fläche der entsprechenden Form zurück. Einige der Bereichsfunktionen werden im Folgenden erläutert:

Fläche der Kreisfunktion : Kreisfläche (A) ist eine Funktion seines Radius(r), sodass gilt:

A = πr ²

Bereich der Dreiecksfunktion : Bereich des Dreiecks (A) ist eine Funktion seiner Basis (b) und Höhe (h), so dass:

A = (bh)/2

Exponentialfunktion

Exponentialfunktion ist diejenige, die als f(x) = e dargestellt wird^X. Es wird oft verwendet, um schnelles Wachstum oder Verfall anzuzeigen.

Logarithmische Funktion

Logarithmische Funktion ist eine mathematische Funktion, die die Umkehroperation der Potenzierung darstellt. Es wird als f(x) = log x dargestellt.

Deckenfunktion

Deckenfunktion , bezeichnet als ⌈x⌉, rundet eine reelle Zahl x auf die nächste ganze Zahl auf, die größer oder gleich x ist. Mit anderen Worten: Es wird der kleinste ganzzahlige Wert gefunden, der größer oder gleich x ist.

Bodenfunktion

Die Bodenfunktion, bezeichnet als ⌊x⌋, rundet eine reelle Zahl x auf die nächste ganze Zahl ab, die kleiner oder gleich x ist. Mit anderen Worten: Es wird der größte ganzzahlige Wert gefunden, der kleiner oder gleich x ist.

Modulfunktion

Modulfunktion , auch Absolutwertfunktion genannt, gibt den Betrag oder die Größe einer reellen Zahl ohne Berücksichtigung ihres Vorzeichens zurück. Die Modulfunktion wird als ∣x∣ bezeichnet, wobei x der Eingabewert ist.

Signum-Funktion

Signum-Funktion , auch Vorzeichenfunktion oder Signumfunktion genannt, ist eine mathematische Funktion, die das Vorzeichen einer reellen Zahl zurückgibt. Es gibt an, ob die Zahl positiv, negativ oder Null ist.

Trigonometrische Funktionen

Trigonometrische Funktionen sind mathematische Funktionen, die die Winkel eines rechtwinkligen Dreiecks mit den Längen seiner Seiten in Beziehung setzen. Die sechs primären trigonometrischen Funktionen sind Sinus (sin), Kosinus (cos), Tangens (tan), Kosekans (cosec), Sekante (sec) und Kotangens (cot).

Komplexe Funktionen

Jede Funktion, deren Eingabevariable eine komplexe Funktion ist, wird als komplexe Funktion bezeichnet. Eine komplexe Zahl ist eine Zahl, die auf der komplexen Ebene dargestellt werden kann. In einem komplexe Zahl Wir haben eine reelle Zahl und eine imaginäre Zahl. Eine komplexe Zahl (z) wird dargestellt als z= x + iy und eine komplexe Funktion wird dargestellt als f(z) = P(x, y) + iQ(x, y)

Anwendungen von Funktionen

Wenn wir sagen, dass eine variable Größe y eine Funktion einer variablen Größe x ist, geben wir an, dass y von x abhängt und dass der Wert von y durch den Wert von x bestimmt wird. Diese Abhängigkeit kann wie folgt ausgedrückt werden: f = y (x).

• Mit dem Radius eines Kreises lässt sich die Fläche eines Kreises berechnen. Der Radius r beeinflusst die Fläche A. Wir erklären, dass A eine Funktion von r in der mathematischen Sprache der Funktionen ist. Wir können A = f(r) =π×r schreiben²
• Das Volumen V einer Kugel ist eine Funktion ihres Radius. V = f(r) = 4/3×r³bezeichnet die Abhängigkeit von V von r.
• Die Kraft ist eine Funktion der Beschleunigung eines Körpers mit der festen Masse m. F = g(a) = m×a.

Die Leute lesen auch:

• Beziehung und Funktion
  
• Bereich und Bereich trigonometrischer Funktionen
• Bereich einer Funktion
• Hyperbolische Funktion

Beispiele zur Funktion

Beispiel 1: Für zwei Funktionen sind f und g definiert als f(x) = x ² und g(x) = ln(2x). Finden Sie die zusammengesetzte Funktion (gof )( x )

Lösung:

Gegeben:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Somit ist (gof)(x) = 2 ln(√2x)

Beispiel 2: Finden Sie die Ausgabe der Funktion g(t)= 6t ² + 5 um

• (i) t = 0
• (ii) t = 2

Lösung:

Gegebene Funktion,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Beispiel 3: Die Länge eines Rechtecks ​​ist fünfmal so groß wie seine Breite. Drücken Sie die Fläche des Rechtecks ​​als Funktion seiner Länge aus.

Lösung:

Die Länge des Rechtecks ​​sei l und die Breite des Rechtecks ​​sei b

Jetzt,

• b = l/5

Fläche des Rechtecks ​​(A) = l × l/5 = l²/5

Somit ist die Fläche eines Rechtecks ​​als Funktion seiner Länge:

A(l) = l ² /5

sortierte Arrayliste Java

Üben Sie Aufgaben zum Thema „Was ist eine Funktion?“.

1. Gegeben sei die Funktion f(x)=3x+5

• Finden Sie f(2)
• Finden Sie f(−1)
• Bestimmen Sie den Bereich und den Bereich der Funktion.

2. Gegeben sei die Funktion g(x)=x ² – 4x + 3

• Finden Sie die Wurzeln der Funktion.
• Finden Sie g(3) und g(0).
• Bestimmen Sie den Scheitelpunkt der Funktion.

3. Gegeben sind zwei Funktionen f(x)=x + 2 und h(x)=2x – 3

• Finden Sie die zusammengesetzte Funktion (f ∘ h) (x)
• Bewerten Sie (f ∘ h)(2)

Zusammenfassung – Was ist eine Funktion?

Eine Funktion ist in der Mathematik eine spezielle Beziehung zwischen Eingabewerten (Domäne) und Ausgabewerten (Bereich), wobei jeder Eingabe eine eindeutige Ausgabe zugeordnet ist. Dargestellt als y = f(x), haben Funktionen spezifische Eigenschaften und können mithilfe geordneter Paare, Tabellen oder Diagramme visualisiert werden. Sie sind bei verschiedenen mathematischen Problemen von wesentlicher Bedeutung und kommen in verschiedenen Formen vor, darunter injektiv (eins zu eins), surjektiv (auf) und bijektiv (beide). Funktionen können mit dem vertikalen Linientest getestet werden und werden weiter in polynomische, inverse, exponentielle, logarithmische und trigonometrische Funktionen klassifiziert. Zum Verständnis von Funktionen gehört das Erkennen ihrer Domäne, ihres Bereichs und der sie definierenden Regeln. Beispiele hierfür sind einfache lineare Funktionen wie y = 2x + 1 und komplexe Funktionszusammensetzungen. Funktionen spielen eine entscheidende Rolle in der Algebra, Geometrie und Analysis und helfen bei der Darstellung und Analyse mathematischer Beziehungen und Phänomene der realen Welt.

FAQs zum Thema „Was ist eine Funktion“.

Was ist die Definition einer Funktion?

Eine auf einer Menge A definierte Beziehung f zu einer anderen Menge B wird in der Mathematik eine Funktion genannt, wenn jeder Wert von A einen eindeutigen Wert in Menge B hat.

Wie schreibe ich eine Funktion in Mathematik?

Die Funktion f wird in der Mathematik als f: A → B dargestellt und ist definiert als: f(x) = x + 2. Hier haben wir für jeden eindeutigen Wert von x einen eindeutigen Wert von y.

Wie transformiere ich eine Funktion?

Wir können eine Funktion leicht in andere Funktionen umwandeln, indem wir einfach grundlegende algebraische Operationen an der Funktion durchführen. Die verschiedenen Transformationen der Funktion sind Spiegelung, Translation, Rotation usw.

Was ist eine rationale Funktion?

Eine Bruchfunktion, bei der Zähler und Nenner Polynomfunktionen sind, wird rationale Funktion genannt. Einige Beispiele für die rationale Funktion sind:

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), usw.

Was ist eine lineare Funktion?

Eine algebraische Funktion, bei der jeder Term der Funktion entweder konstant ist oder eine Potenz von Eins hat, wird als lineare Funktion bezeichnet. Einige Beispiele für die lineare Funktion sind:

• f(x) = 2x + 3
• g(x) = x – 5 usw.

Was sind Domäne und Kodomäne einer Funktion?

Wenn wir die Funktion definieren als: y = f(x). Dann umfasst der Definitionsbereich von x alle Werte von x, für die y einen eindeutigen Wert ergibt. Und der Co-Bereich von y ist die Menge aller Werte von y für jeden Wert von x.

Wie erkennt man eine Funktion in der Mathematik?

Wenn ein Eingabewert (x) der Domäne in einer Beziehung mehr als ein Bild (y) hat, kann diese Beziehung niemals eine Funktion sein. Wenn also der Wert von x im geordneten Paar wiederholt wird, ist es niemals eine Funktion.