Polygon in der Mathematik ist eine zweidimensionale Form, die aus geraden Linien besteht, die eine geschlossene Polygonkette bilden. Das Wort Polygon kommt von den Wörtern poly und gon, die viele und Seiten bedeuten.
Polygone können einfach oder sich selbst schneidend sein. Ein einfaches Polygon schneidet sich selbst nicht, außer an den gemeinsamen Endpunkten aufeinanderfolgender Segmente. Eine Polygonkette, die sich selbst kreuzt, erzeugt ein sich selbst schneidendes Polygon. Polygone können auch als konkav oder konvex klassifiziert werden.
In diesem Artikel haben wir ausführlich über Polygone und ihre Typen, Formeln und Beispiele gesprochen.
| Wichtige Fakten über Polygone | |
|---|---|
| Summe der Innenwinkel eines Polygons | (n–2) × 180° |
| Anzahl der Diagonalen im Polygon | n(n–3)/2 |
| Innenwinkel eines regelmäßigen Polygons Was ist ein Linux-Dateisystem? | {(n–2) × 180°}/n |
| Außenwinkel eines regelmäßigen Polygons | 360°/n |
Inhaltsverzeichnis
- Was sind Polygone?
- Polygondiagramm basierend auf der Anzahl der Seiten
- Eigenschaften von Polygonen
- Polygonformen
- Arten von Polygonen
- Polygonformeln
- Winkel in Polygonen
- FAQs
Was sind Polygone?
Der Begriff „Polygon“ stammt vom griechischen Wort polugonos ab, wobei „poly“ „viele“ und „gon“ „Winkel“ bedeutet. Im Allgemeinen ist ein Polygon eine geschlossene Figur, die aus geraden Linien besteht und deren Innenwinkel durch diese gebildet werden Linien. Um eine geschlossene Form zu bilden, sind mindestens drei Liniensegmente erforderlich. Es wird allgemein als Dreieck oder Dreieck bezeichnet. Der allgemeine Begriff für ein n-seitiges Polygon ist ein n-Eck.
Polygondefinition
Polygone sind flache, zweidimensionale Figuren, die aus geraden Seiten bestehen, die eine vollständig geschlossene Form bilden. In der Geometrie ist das Polygon eine ebene Figur, die aus Liniensegmenten besteht, die zu einer geschlossenen Polygonkette verbunden sind. Sie bestehen aus geraden Seiten, nicht aus Kurven, und können beliebig viele Seiten haben. Einige Polygone unterschiedlicher Art sind: offen, nur begrenzt, geschlossen und sich selbst schneidend.
In der Geometrie wird ein Polygon als geschlossene, zweidimensionale Form definiert, die flach in einer Ebene liegt und von geraden Seiten umgeben ist.
Einem Polygon fehlen gekrümmte Seiten und seine Kanten sind die geraden Segmente, die seine Grenze definieren. Die Treffpunkte dieser Kanten werden als Eckpunkte oder Eckpunkte bezeichnet.
Polygon-Beispiele
Aus mathematischer Sicht sind Dreiecke, Sechsecke, Fünfecke und Vierecke Beispiele für Polygone. Beispiele für Polygon aus dem wirklichen Leben sind rechteckige Bildschirme auf Ihrem Laptop, Fernseher oder Mobiltelefon; rechteckiger Fußballplatz oder Spielplatz, Bermuda-Dreieck und ägyptische Pyramiden in dreieckiger Form.

Teile eines Polygons
Ein Polygon besteht aus drei grundlegenden Komponenten:
- Seiten des Polygons: Die Seiten eines Polygons sind die Grenzen der Polygone, die den geschlossenen Bereich definieren.
- Eckpunkte: Der Punkt, an dem sich zwei Seiten treffen, wird als Scheitelpunkt bezeichnet.
- Winkel: Das Polygon enthält sowohl Innen- als auch Außenwinkel. Durch den Schnittpunkt seiner Seiten wird innerhalb des umschlossenen Bereichs des Polygons ein Innenwinkel gebildet.
Polygondiagramm basierend auf der Anzahl der Seiten
Nomenklatur von Polygonen, definiert auf der Grundlage der Anzahl ihrer Seiten. Es wird als N-Ecke bezeichnet, wobei „n“ die Anzahl der Seiten angibt. Polygone werden im Allgemeinen anhand der Anzahl ihrer Kanten identifiziert. Beispielsweise wird ein Polygon mit fünf Seiten als 5-Eck bezeichnet, während eines mit zehn Seiten als 10-Eck bezeichnet wird.
| Polygondiagramm | ||||
|---|---|---|---|---|
| Namen von Polygonformen | Anzahl der Seiten | Anzahl der Eckpunkte | Anzahl der Diagonalen | Innenwinkelmaß für regelmäßige Form |
| Dreieck | Polygone mit 3 Seiten | 3 | 0 | 60° |
| Viereck | Polygone mit 4 Seiten | 4 | 2 | 90° |
| Pentagon | Polygone mit 5 Seiten | 5 | 5 | 108° |
| Hexagon | Polygone mit 6 Seiten | 6 | 9 | 120° |
| Heptagon | Polygone mit 7 Seiten | 7 | 14 | 128,571° |
| Achteck | Polygone mit 8 Seiten | 8 | zwanzig | 135° |
| Nonagon | Polygone mit 9 Seiten | 9 | 27 | 140° |
| Zehneck | Polygone mit 10 Seiten | 10 | 35 | 144° |
| Hendecagon | Polygone mit 11 Seiten | elf | 44 | 147,273° |
| Zwölfeck | Polygone mit 12 Seiten | 12 | 54 | 150° |
Eigenschaften von Polygonen
Die Eigenschaften von Polygonen lassen sich leicht identifizieren. Die folgenden Eigenschaften tragen dazu bei, die Polygone leicht zu kennen:
- Ein Polygon ist eine geschlossene Form ohne offene Enden. Ursprung und Endpunkt sollten gleich sein.
- Es nimmt eine flächige Form an, die aus Liniensegmenten oder geraden Linien besteht, die gemeinsam die Figur formen.
- Als zweidimensionale Einheit existiert ein Polygon nur in den Dimensionen Länge und Breite, ohne Tiefe oder Höhe.
- Es besitzt drei oder mehr Seiten, um ein Polygon zu bilden.
- Die Winkel im Polygon können variieren. Es zeigt eine ausgeprägte Konfiguration.
- Die Länge der Seiten eines Polygons kann variieren; Es kann im gesamten Polygon gleich sein oder auch nicht.
Polygonformen
Ein Polygon ist eine flache, zweidimensionale Form, die durch gerade Seiten gekennzeichnet ist, die zu einer geschlossenen Figur verbunden sind. Beispiele für Polygonformen sind:
- Dreieck
- Viereck
- Pentagon
- Hexagon
- Heptagon
- Achteck
- Nonagon
- Zehneck
Dreieck
- Es hat 3 Seiten und 3 Eckpunkte.
- Es hat keine Diagonalen.
- Die Summe des Innenraums beträgt 180°.
Viereck
- Es hat 4 Seiten und 4 Eckpunkte.
- Es hat 2 Diagonalen.
- Die Summe der Innenwinkel beträgt 360°.
Pentagon
- Es hat 5 Seiten und 5 Eckpunkte.
- Es hat 5 Diagonalen.
- Die Summe der Innenwinkel beträgt 540°.
Hexagon
- Es hat 6 Seiten und 6 Eckpunkte.
- Es hat 9 Diagonalen.
- Die Summe der Innenwinkel beträgt 720°.
Heptagon
- Es hat 7 Seiten und 7 Eckpunkte.
- Es hat 14 Diagonalen.
- Die Summe der Innenwinkel beträgt 900°.
Achteck
- Es hat 8 Seiten und 8 Eckpunkte.
- Es hat 20 Diagonalen.
- Die Summe der Innenwinkel beträgt 1080°.
Nonagon
- Es hat 9 Seiten und 9 Eckpunkte.
- Es hat 27 Diagonalen.
- Die Summe der Innenwinkel beträgt 1260°.
Zehneck
- Es hat 10 Seiten und 10 Eckpunkte.
- Es hat 35 Diagonalen.
- Die Summe der Innenwinkel beträgt 1440°.
Arten von Polygonen
Abhängig von den Seiten und Winkeln können die Polygone auf unterschiedlicher Grundlage in verschiedene Typen eingeteilt werden, wie zum Beispiel:
- Auf der Grundlage von Seiten
- Auf der Grundlage von Winkeln
- Auf der Grundlage der Grenze
Polygone auf Basis von Seiten
Polygone können anhand der Eigenschaften ihrer Seiten in zwei Haupttypen eingeteilt werden:
- Regelmäßiges Vieleck
- Unregelmäßiges Polygon
Regelmäßiges Vieleck
Ein regelmäßiges Polygon zeichnet sich dadurch aus, dass alle Seiten gleich lang und alle Innenwinkel gleich groß sind. Es kann sowohl gleichseitig als auch gleichwinklig sein. Beispiele für regelmäßige Vielecke sind das Dreieck, das Viereck, das Fünfeck und das Sechseck.

Regelmäßiges Vieleck
Unregelmäßiges Polygon
Ein unregelmäßiges Polygon hat ungleich lange Seiten und Winkel unterschiedlicher Größe. Jedes Polygon, das nicht den Kriterien eines regelmäßigen Polygons entspricht, wird als unregelmäßig klassifiziert. Häufige Beispiele für unregelmäßige Polygone sind das ungleichseitige Dreieck, Vierecke wie Rechteck, Trapez oder Drachen sowie unregelmäßige Fünfeck- und Sechseckstrukturen.
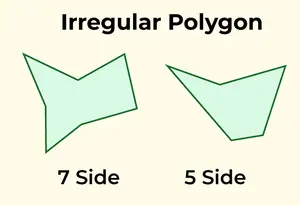
Unregelmäßiges Polygon
Polygone auf Basis von Winkeln
Polygone können aufgrund der Art ihrer Winkel in zwei Hauptkategorien eingeteilt werden:
- Konvexes Polygon
- Konkaves Polygon
Konvexes Polygon
Ein konvexes Polygon hat keinen Innenwinkel, der mehr als 180° beträgt. Konvexe Polygone können drei oder mehr Seiten haben. Bei konvexen Polygonen liegen alle Diagonalen innerhalb der geschlossenen Figur. Gängige Beispiele für konvexe Polygone sind Dreiecke, alle konvexen Vierecke sowie regelmäßige Fünfecke und Sechsecke
Konkaves Polygon
Ein konkaves Polygon hat mindestens einen Innenwinkel, der ein Reflexwinkel ist und nach innen zeigt. Konkave Polygone haben mindestens vier Seiten. Dieser Polygontyp weist mindestens einen Innenwinkel auf, der mehr als 180° beträgt. Bei konkaven Polygonen erstrecken sich einige Diagonalen über die eingeschlossene Figur hinaus. Beispiele für konkave Polygone sind ein Pfeil oder eine Pfeilspitze in Vierecken sowie bestimmte unregelmäßige Fünf- und Sechsecke.
Unterschied zwischen konkaven und konvexen Polygonen
Sehen wir uns den Unterschied zwischen konvexem und konkavem Polygon in der folgenden Tabelle an:

| Konvexes Polygon | Konkaves Polygon |
|---|---|
| Der gesamte Umfang einer konvexen Form erstreckt sich nach außen, ohne Einkerbungen nach innen. | Eine konkave Form weist mindestens einen nach innen gerichteten Teil auf, der auf das Vorhandensein einer Delle hinweist. |
| In einem konvexen Polygon liegen alle Innenwinkel unter 180°. | In einem konkaven Polygon gibt es mindestens einen Innenwinkel, der 180° überschreitet. |
| Jede Linie, die zwei Eckpunkte einer konvexen Form verbindet, liegt vollständig innerhalb der Grenzen der Form. | Die Linie, die zwei beliebige Eckpunkte einer konkaven Form verbindet, kann das Innere der Form schneiden oder auch nicht. |
Polygone auf Basis von Grenzen
Polygone können basierend auf der Art ihrer Grenzen in zwei Haupttypen eingeteilt werden:
- Einfaches Polygon
- Komplexes Polygon
Einfaches Polygon
Ein einfaches Polygon zeichnet sich durch eine singuläre, sich nicht schneidende Grenze aus. Mit anderen Worten, es überschreitet sich nicht selbst und besteht aus einer Grenze.
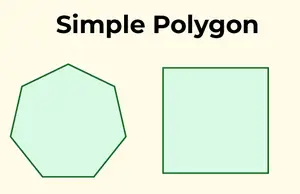
Einfache Polygone
Komplexes Polygon
Andererseits wird ein komplexes Polygon dadurch definiert, dass es sich selbst überschneidet. Es besteht aus mehr als einer Grenze innerhalb seiner Struktur. Bei komplexen Polygonen überschneidet sich die Grenze, wodurch mehrere unterschiedliche Bereiche innerhalb des Polygons entstehen.

Komplexes Polygon
Lesen Sie mehr über Arten von Polygonen.
Polygonformeln
Es gibt mehrere Formeln für Polygone in der Geometrie. Zu den am häufigsten verwendeten gehören:
- Flächenformel
- Umfangsformel
- Anzahl der Diagonalen
Alle Formeln, die sich auf verschiedene Polygone beziehen, werden im Folgenden erläutert:
Bereich der Polygone
Fläche eines Polygons stellt den Gesamtraum dar, den es in einer zweidimensionalen Ebene einnimmt, und wird durch spezifische Formeln bestimmt, die auf der Anzahl der Seiten und der Klassifizierung des Polygons basieren. Die Flächenformeln lauten wie folgt:
| Bereich des Polygons | Formel |
|---|---|
| Bereich des Dreiecks | 1/2 × Basis × Höhe |
| Fläche des Parallelogramms | Basis × Höhe |
| Fläche eines Rechtecks | Länge × Breite |
| Fläche des Platzes | (Seite)2 |
| 1/2 × Diagonale1× Diagonale2 | |
| Bereich des Trapezes | 1/2 × Höhe × Summe paralleler Seiten |
| (5/2) × Seitenlänge × Apothem | |
| Bereich des Sechsecks | {(3√3)/2}Seite2 |
| Fläche von Heptagon | 3,643 × Seite2 |
Umfang von Polygonen
Der Umfang einer zweidimensionalen Form stellt die Gesamtlänge ihrer äußeren Begrenzung dar. Für Polygone wird der Umfang wie folgt berechnet:
| Umfang des Polygons | Formel |
|---|---|
| Umfang des Dreiecks | Summe dreier Seiten |
| Umfang des Parallelogramms | 2 (Summe benachbarter Seiten) |
| Umfang des Rechtecks | 2(Länge + Breite) |
| Umfang des Quadrats | 4 × Seite |
| Umfang der Raute | 4 × Seite |
| Umfang des Trapezes | Summe paralleler Seiten + Summe nicht paralleler Seiten |
| Umfang des Pentagons | 5 × Seite |
| Umfang des Sechsecks | 6 × Seite |
| Umfang des Siebenecks | 7 × Seite |
Diagonale der Polygonformel
Eine Diagonale eines Polygons ist ein Liniensegment, das durch die Verbindung zweier nicht benachbarter Eckpunkte gebildet wird.
Anzahl der Diagonalen in einem Polygon = n(n−3)/2,
Wobei „n“ die Anzahl der Seiten darstellt, die das Polygon besitzt.
Lesen Sie mehr über Diagonale der Polygonformel .
Winkel in Polygonen
In der Geometrie beziehen sich Winkel in Polygonen auf die Winkel, die von den Seiten eines Polygons gebildet werden, sowohl im Inneren als auch im Äußeren des Polygons. Somit kann es im Polygon beide Winkel geben, d.h.
- Innenwinkel
- Außenwinkel
Lassen Sie uns die Formel für diese Winkel im Detail wie folgt besprechen:
Innenwinkelformel von Polygonen
Die Innenwinkel eines Polygons sind diejenigen, die zwischen seinen benachbarten Seiten gebildet werden, und sind im Fall eines regelmäßigen Polygons gleich. Die Anzahl der Innenwinkel entspricht der Anzahl der Seiten im Polygon.
Die Summe der Innenwinkel „S“ in einem Polygon mit „n“ Seiten wird berechnet als:
S = (n – 2) × 180°
Wobei „n“ die Anzahl der Seiten darstellt.
Außenwinkelformel von Polygonen
Jeder Außenwinkel eines regelmäßigen Polygons wird gebildet, indem eine seiner Seiten verlängert wird (entweder im oder gegen den Uhrzeigersinn) und der Winkel zwischen dieser Verlängerung und der angrenzenden Seite gemessen wird. In einem regelmäßigen Vieleck sind alle Außenwinkel gleich
Die Gesamtsumme der Außenwinkel in jedem Polygon ist auf 360° festgelegt
Daher,
Jeder Außenwinkel ist durch 360°/n gegeben
Wobei „n“ die Anzahl der Seiten ist.
Die Summe der Innen- und entsprechenden Außenwinkel an jedem Scheitelpunkt in einem Polygon beträgt immer 180 Grad und drückt eine ergänzende Beziehung aus:
Innenwinkel + Außenwinkel = 180°
Außenwinkel = 180° – Innenwinkel
Abschluss
- Ein Polygon ist eine geschlossene Figur, die durch drei oder mehr Liniensegmente begrenzt wird
- Summe der Innenwinkel: Die Summe aller Innenwinkel in einem n-seitigen Polygon ergibt sich aus der Formel (n–2)×180°.
- Anzahl der Diagonalen: Für ein Polygon mit n Seiten wird die Anzahl der Diagonalen mit der Formel n(n–3)/2 berechnet.
- Durch Diagonalen gebildete Dreiecke: Die Anzahl der Dreiecke, die durch die Verbindung von Diagonalen von einer einzelnen Ecke eines Polygons gebildet werden, beträgt n–2.
- Innenwinkel eines regelmäßigen Polygons: Das Maß jedes Innenwinkels in einem n-seitigen regelmäßigen Polygon beträgt {(n–2)×180°}/n.
- Außenwinkel eines regelmäßigen Polygons: Das Maß jedes Außenwinkels in einem n-seitigen regelmäßigen Polygon beträgt 360°/n.
Lesen Sie auch
- Quadrat
- Parallelogramm
- Rechteck
Gelöste Beispiele zu Polygonen in der Mathematik
Beispiel 1: Betrachten Sie ein Viereck mit vier Seiten. Finden Sie die Summe aller Innenwinkel des Vierecks.
Lösung:
Formel für die Summe der Innenwinkel in einem n-seitigen regelmäßigen Vieleck = (n − 2) × 180°
Die Summe aller Innenwinkel des Vierecks = (4 – 2) × 180°
Die Summe aller Innenwinkel des Vierecks = 2 × 180°
Die Summe aller Innenwinkel des Vierecks = 360°
Daher beträgt die Summe aller Innenwinkel des Vierecks 360°.
Beispiel 2: Betrachten Sie ein regelmäßiges Polygon mit einem gegebenen Außen- und Innenwinkelverhältnis von 7:3. Bestimmen Sie die Art des Polygons.
Lösung:
Das Verhältnis von Außen- und Innenwinkel beträgt 7:3.
Nehmen Sie an, dass der Außen- und Innenwinkel eines Polygons 7x und 3x beträgt.
Die Summe der Außen- und Innenwinkel eines Polygons beträgt 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Außenwinkel = 18°
Anzahl der Seiten = 360°/Außenwinkel
= 360°/18°
= 20
Daher ist das gegebene Polygon ein Ikosagon, da es 20 Seiten hat.
Beispiel 3: Jeder Außenwinkel eines Polygons misst 90 Grad. Bestimmen Sie den Typ des Polygons?
Lösung:
Gemäß der Formel ist jeder Außenwinkel = 360°/n
Hier ist n=Anzahl Seiten.
90°= 360°/n
n = 360°/90°= 4
Daher ist das betreffende Polygon ein Viereck, da es vier Seiten besitzt.
Beispiel 4: Die Seiten sind 10 m, 10 m, 8 m, 8 m, 5 m, 5 m, 9 m, 9 m. Wie viele Meter Seil werden für den Perimeter benötigt?
Lösung:
Um die Länge des Seils zu ermitteln, die für den Umfang benötigt wird, müssen wir die Längen aller Seiten summieren:
Umfang = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Umfang = 64 m.
Daher werden für den Perimeter insgesamt 64 Meter Seil benötigt.
Übungsfragen zu Polygonen in der Geometrie
Im Folgenden finden Sie einige Übungsfragen, die auf der Formel von Polygonen basieren:
Q1. Angenommen, ein Winkel eines Fünfecks beträgt 140°. Bestimmen Sie die Größe des größten Winkels, wenn die übrigen Winkel im Verhältnis 1:2:3:4 stehen.
Q2. Wenn die Summe der Innenwinkel eines Polygons 160° beträgt, ermitteln Sie die Anzahl der Seiten im Polygon.
Q3. Die Anzahl der Seiten in zwei regelmäßigen Vielecken steht im Verhältnis 2:3 und das Verhältnis ihrer Innenwinkel beträgt 4:5. Finden Sie die jeweilige Anzahl der Seiten dieser Polygone.
Q4. Bestimmen Sie die Gesamtwinkelsumme in einem Siebeneck.
F5. Berechnen Sie die Summe der Außenwinkel in einem Fünfeck.
F6. Wie viele Seiten hat ein Sechseck?
- 4
- 6
- 8
- 10
F7. Welches der folgenden ist kein regelmäßiges Polygon?
- Dreieck
- Quadrat
- Pentagon
- Parallelogramm
FAQs zu Polygonen in der Mathematik
Was ist ein Polygon in der Mathematik?
In der Mathematik bezeichnet ein Polygon eine geschlossene zweidimensionale Figur, die durch die Verbindung von drei oder mehr geraden Linien entsteht. Der Begriff Polygon leitet sich aus dem Griechischen ab, wobei „poly“ für „viele“ und „gon“ für „Winkel“ steht.
Welches ist das kleinste Polygon?
Das kleinste gebildete Polygon ist ein Dreieck mit drei Seiten.
Was ist 20-Eck?
Ein 20-Eck ist ein zwanzigseitiges Polygon in der Geometrie.
Wie groß ist die Gesamtsumme der Außenwinkel eines Polygons?
Die Summe der Außenwinkel eines Polygons beträgt 360°.
Kann ein Kreis als Polygon klassifiziert werden?
Ein Polygon ist eine geschlossene Form, die aus geraden Segmenten besteht. Der Kreis ist eine geschlossene Figur, besteht aber aus einer Kurve. Ein Kreis ist also kein Polygon.
Was ist die Summe der Innenwinkel eines Polygons?
Die Summe der Innenwinkel eines Polygons ergibt sich aus (n–2)×180°, wobei n die Anzahl der Seiten im Polygon ist.
