logo

TechCodeview

Algorithmen-Tutorial

Algorithmus ist ein schrittweises Vorgehen zur Lösung eines Problems oder zur Erledigung einer Aufgabe. Im Kontext von Datenstrukturen und Algorithmen handelt es sich um eine Reihe genau definierter Anweisungen zur Ausführung einer bestimmten Rechenaufgabe. Algorithmen sind von grundlegender Bedeutung für die Informatik und spielen eine sehr wichtige Rolle bei der Entwicklung effizienter Lösungen für verschiedene Probleme. Das Verständnis von Algorithmen ist für jeden, der sich für die Beherrschung von Datenstrukturen und Algorithmen interessiert, von entscheidender Bedeutung.

Was ist ein Algorithmus?

Inhaltsverzeichnis



boto3

Was ist ein Algorithmus?

Ein Algorithmus ist eine endliche Folge wohldefinierter Anweisungen, die zur Lösung eines Rechenproblems verwendet werden können. Es bietet eine Schritt-für-Schritt-Anleitung, mit der eine Eingabe in eine gewünschte Ausgabe umgewandelt wird.

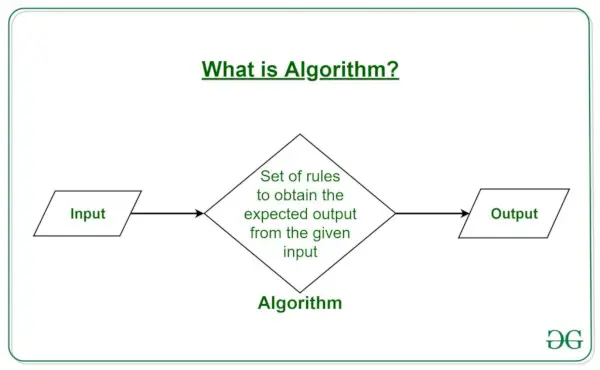
Wie funktionieren Algorithmen?

Algorithmen folgen typischerweise einer logischen Struktur:

  • Eingang: Der Algorithmus empfängt Eingabedaten.
  • Wird bearbeitet: Der Algorithmus führt eine Reihe von Operationen an den Eingabedaten durch.
  • Ausgabe: Der Algorithmus erzeugt die gewünschte Ausgabe.

Eigenschaften eines Algorithmus:

  • Klar und eindeutig: Der Algorithmus sollte eindeutig sein. Jeder seiner Schritte sollte in allen Aspekten klar sein und darf nur zu einer Bedeutung führen.
  • Gut definierte Eingaben: Wenn ein Algorithmus vorgibt, Eingaben entgegenzunehmen, sollten es wohldefinierte Eingaben sein. Es kann Eingaben annehmen oder auch nicht.
  • Gut definierte Ausgaben: Der Algorithmus muss klar definieren, welche Ausgabe erzielt wird, und er sollte auch klar definiert sein. Es sollte mindestens 1 Ausgabe erzeugen.
  • Endlichkeit: Der Algorithmus muss endlich sein, d. h. er sollte nach einer endlichen Zeit terminieren.
  • Machbar: Der Algorithmus muss einfach, generisch und praktisch sein, sodass er mit angemessenen Einschränkungen und Ressourcen ausgeführt werden kann.
  • Sprachunabhängig: Der Algorithmus muss sprachunabhängig sein, d. h. es müssen lediglich einfache Anweisungen sein, die in jeder Sprache implementiert werden können, und dennoch wird die Ausgabe erwartungsgemäß dieselbe sein.

Was ist der Bedarf an Algorithmen?

Algorithmen sind für die effiziente und effektive Lösung komplexer Rechenprobleme unerlässlich. Sie bieten einen systematischen Ansatz für:

Formatieren Sie ein Datum in Java
  • Probleme lösen: Algorithmen zerlegen Probleme in kleinere, überschaubare Schritte.
  • Optimierungslösungen: Algorithmen finden die besten oder nahezu optimalen Lösungen für Probleme.
  • Aufgaben automatisieren: Algorithmen können sich wiederholende oder komplexe Aufgaben automatisieren und so Zeit und Aufwand sparen.

Beispiele für Algorithmen

Nachfolgend finden Sie einige Beispiele für Algorithmen:

Bilderspiele für Android
  • Sortieralgorithmen: Sortierung zusammenführen, Schnellsortierung, Heap-Sortierung
  • Suchalgorithmen: Lineare Suche, Binäre Suche, Hashing
  • Graphalgorithmen: Dijkstra-Algorithmus, Prim-Algorithmus, Floyd-Warshall-Algorithmus
  • String-Matching-Algorithmen: Knuth-Morris-Pratt-Algorithmus, Boyer-Moore-Algorithmus

Wie schreibe ich einen Algorithmus?

Um einen Algorithmus zu schreiben, gehen Sie folgendermaßen vor:

  • Definiere das Problem: Geben Sie das zu lösende Problem klar an.
  • Entwerfen Sie den Algorithmus: Wählen Sie ein geeignetes Algorithmus-Design-Paradigma und entwickeln Sie eine schrittweise Vorgehensweise.
  • Implementieren Sie den Algorithmus: Übersetzen Sie den Algorithmus in eine Programmiersprache.
  • Testen und debuggen: Führen Sie den Algorithmus mit verschiedenen Eingaben aus, um seine Korrektheit und Effizienz sicherzustellen.
  • Analysieren Sie den Algorithmus: Bestimmen Sie die zeitliche und räumliche Komplexität und vergleichen Sie sie mit alternativen Algorithmen.

Lernen Sie die Grundlagen von Algorithmen

Analyse von Algorithmen

  • Asymptotische Analyse
  • Worst, Average und Best Cases
  • Asymptotische Notationen
  • Untere und obere Schrankentheorie
  • Einführung in die amortisierte Analyse
  • Was bedeutet „Weltraumkomplexität“?
  • Polynomiales Zeitnäherungsschema
  • Buchhaltungsmethode | Amortisierte Analyse
  • Potenzielle Methode in der amortisierten Analyse

Arten von Algorithmen

Algorithmen können unterschiedlicher Art sein, je nachdem, was sie tun und wie sie erstellt werden. Einige gängige Typen sind:

1. Such- und Sortieralgorithmen

  • Einführung in Suchalgorithmen
  • Einführung in den Sortieralgorithmus
  • Stabile und instabile Sortieralgorithmen
  • Untergrenze für vergleichsbasierte Sortieralgorithmen
  • Kann die Laufzeitkomplexität eines vergleichsbasierten Sortieralgorithmus weniger als N logN betragen?
  • Welcher Sortieralgorithmus führt die minimale Anzahl an Speicherschreibvorgängen durch?

2. Gierige Algorithmen

3. Dynamische Programmieralgorithmen

  • Einführung in die dynamische Programmierung
  • Eigenschaft „Überlappende Teilprobleme“.
  • Optimale Unterkonstruktionseigenschaft
  • Längste ansteigende Folge
  • Längste gemeinsame Folge
  • Min. Kostenpfad
  • Münzwechsel
  • Matrixkettenmultiplikation
  • 0-1 Rucksackproblem
  • Längste palindromische Folge
  • Palindrom-Partitionierung

4. Mustersuchalgorithmen

  • Einführung in die Mustersuche
  • Naive Mustersuche
  • KMP-Algorithmus
  • Rabin-Karp-Algorithmus
  • Mustersuche mithilfe eines Versuchs aller Suffixe
  • Aho-Corasick-Algorithmus zur Mustersuche
  • Z-Algorithmus (Algorithmus zur Suche nach linearen Zeitmustern)

5. Backtracking-Algorithmus

  • Einführung in das Backtracking
  • Gibt alle Permutationen einer bestimmten Zeichenfolge aus
  • Das Tourproblem des Ritters
  • Ratte in einem Labyrinth
  • N-Queen-Problem
  • Teilmengensumme
  • m Farbproblem
  • Hamilton-Zyklus
  • Sudoku

6. Divide-and-Conquer-Algorithmus

7. Geometrischer Algorithmus

  • Einführung in geometrische Algorithmen
  • Nächstes Punktepaar | O(nlogn)-Implementierung
  • Wie kann man überprüfen, ob ein bestimmter Punkt innerhalb oder außerhalb eines Polygons liegt?
  • Wie kann man überprüfen, ob sich zwei gegebene Liniensegmente schneiden?
  • Finden Sie bei gegebenen n Liniensegmenten, ob sich zwei beliebige Segmente schneiden
  • So überprüfen Sie, ob vier gegebene Punkte ein Quadrat bilden
  • Konvexer Rumpf unter Verwendung des Jarvis-Algorithmus oder Wrapping

8. Mathematische Algorithmen

  • Einführung in mathematische Algorithmen
  • Schreiben Sie eine effiziente Methode, um zu prüfen, ob eine Zahl ein Vielfaches von 3 ist
  • Schreiben Sie ein Programm, um zwei Zahlen zur Basis 14 zu addieren
  • Programm für Fibonacci-Zahlen
  • Durchschnitt eines Zahlenstroms
  • Multiplizieren Sie zwei Ganzzahlen ohne Verwendung von Multiplikations-, Divisions- und bitweisen Operatoren und ohne Schleifen
  • Babylonische Methode zur Quadratwurzel
  • Sieb des Eratosthenes
  • Pascals Dreieck
  • Finden Sie anhand einer gegebenen Zahl das nächstkleinere Palindrom
  • Programm zum Addieren zweier Polynome
  • Multiplizieren Sie zwei Polynome
  • Zählen Sie nachgestellte Nullen in der Fakultät einer Zahl

9. Bitweise Algorithmen

  • Einführung in bitweise Algorithmen
  • Little und Big Endian
  • Erkennen Sie entgegengesetzte Vorzeichen
  • Bits tauschen
  • Deaktivieren Sie das ganz rechts gesetzte Bit
  • Bits drehen
  • Nächsthöhere Zahl mit gleicher Anzahl gesetzter Bits
  • Tauschen Sie zwei Nibbles in einem Byte aus

10. Graphalgorithmen

12. Branch-and-Bound-Algorithmen

  • Verzweigt und gebunden | Set 1 (Einführung mit 0/1 Rucksack)
  • Verzweigt und gebunden | Set 2 (Implementierung von 0/1 Rucksack)
  • Verzweigt und gebunden | Satz 3 (8-Puzzle-Aufgabe)
  • Zweig und gebunden | Satz 4 (Aufgabenzuweisungsproblem)
  • Verzweigt und gebunden | Satz 5 (N-Queen-Problem)
  • Zweig und gebunden | Satz 6 (Problem des Handlungsreisenden)

Quiz:

  • Analyse von Algorithmen
  • Sortierung
  • Teilen und erobern
  • Gierige Algorithmen
  • Dynamische Programmierung
  • Zurückverfolgen
  • NP abgeschlossen
  • Suchen
  • Rekursion
  • Bit-Algorithmen